题目内容
已知等比数列an中,公比 .
.
(I)求数列an的通项公式;
(II)求数列bn的前n项和Sn.
解:(I)由题意知 解方程组:
解方程组:
∵q∈(0,1)
∴a2>a4
∴
∴
∴
所以数列an的通项公式为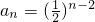
(II) ,
,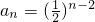
∴

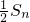 =
=

两式相减得
解得
数列bn的前n项和
分析:(I)利用等比数列的性质得到 ,列出关于a2,a4的方程组,求出a2,a4;求出首项与公比,利用等比数列的通项公式求出通项
,列出关于a2,a4的方程组,求出a2,a4;求出首项与公比,利用等比数列的通项公式求出通项
(II)数列的通项是一个等比数列与一个等差数列的积构成的新数列,利用错位相减法求出数列的前n项和.
点评:求数列的前n项和时,关键是判断出通项的特点,据通项的特点选择合适的求和方法.
 解方程组:
解方程组:
∵q∈(0,1)
∴a2>a4
∴

∴

∴

所以数列an的通项公式为
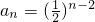
(II)
 ,
,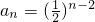
∴


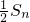 =
=

两式相减得

解得

数列bn的前n项和

分析:(I)利用等比数列的性质得到
 ,列出关于a2,a4的方程组,求出a2,a4;求出首项与公比,利用等比数列的通项公式求出通项
,列出关于a2,a4的方程组,求出a2,a4;求出首项与公比,利用等比数列的通项公式求出通项(II)数列的通项是一个等比数列与一个等差数列的积构成的新数列,利用错位相减法求出数列的前n项和.
点评:求数列的前n项和时,关键是判断出通项的特点,据通项的特点选择合适的求和方法.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目