题目内容
(本题12分)已知椭圆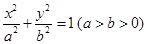 的长半轴长为
的长半轴长为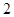 ,且点
,且点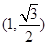 在椭圆上.
在椭圆上.
(1)求椭圆的方程;
(2)过椭圆右焦点的直线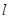 交椭圆于
交椭圆于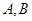 两点,若
两点,若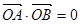 ,求直线
,求直线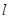 方程.
方程.
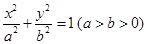 的长半轴长为
的长半轴长为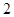 ,且点
,且点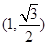 在椭圆上.
在椭圆上.(1)求椭圆的方程;
(2)过椭圆右焦点的直线
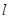 交椭圆于
交椭圆于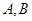 两点,若
两点,若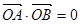 ,求直线
,求直线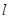 方程.
方程.解:(Ⅰ)由题意:  .所求椭圆方程为
.所求椭圆方程为 .
.
又点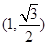 在椭圆上,可得
在椭圆上,可得 .所求椭圆方程为
.所求椭圆方程为 .(4分)
.(4分)
(Ⅱ)由(Ⅰ)知 ,又
,又 ,所以
,所以 ,椭圆右焦点为
,椭圆右焦点为 .
.
因为 .若直线
.若直线 的斜率不存在,则直线
的斜率不存在,则直线 的方程为
的方程为 .
.
直线 交椭圆于
交椭圆于 两点,
两点,  ,不合题意.(6分)
,不合题意.(6分)
若直线 的斜率存在,设斜率为
的斜率存在,设斜率为 ,则直线
,则直线 的方程为
的方程为 .
.
由 可得
可得 .
.
由于直线 过椭圆右焦点,可知
过椭圆右焦点,可知 .
.
设 ,则
,则 ,(8分)
,(8分)
 .
.
所以 .
.
由 ,即
,即 ,可得
,可得 .(11分)
.(11分)
所以直线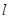 的方程为
的方程为 . (12分)
. (12分)
 .所求椭圆方程为
.所求椭圆方程为 .
.又点
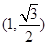 在椭圆上,可得
在椭圆上,可得 .所求椭圆方程为
.所求椭圆方程为 .(4分)
.(4分)(Ⅱ)由(Ⅰ)知
 ,又
,又 ,所以
,所以 ,椭圆右焦点为
,椭圆右焦点为 .
.因为
 .若直线
.若直线 的斜率不存在,则直线
的斜率不存在,则直线 的方程为
的方程为 .
.直线
 交椭圆于
交椭圆于 两点,
两点,  ,不合题意.(6分)
,不合题意.(6分)若直线
 的斜率存在,设斜率为
的斜率存在,设斜率为 ,则直线
,则直线 的方程为
的方程为 .
.由
 可得
可得 .
.由于直线
 过椭圆右焦点,可知
过椭圆右焦点,可知 .
.设
 ,则
,则 ,(8分)
,(8分) .
.所以
 .
.由
 ,即
,即 ,可得
,可得 .(11分)
.(11分)所以直线
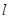 的方程为
的方程为 . (12分)
. (12分) 略

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
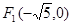 ,
,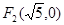 ,
,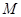 是椭圆上一点,
是椭圆上一点,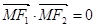 ,
,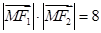 ,则该椭圆的方程是( )
,则该椭圆的方程是( ) 



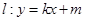 与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过 椭圆C的右顶点.求证:直线l过定点,并求该定点的坐标.
与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过 椭圆C的右顶点.求证:直线l过定点,并求该定点的坐标.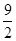 ,并且与直线
,并且与直线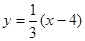 相交所得线段中点的横坐标为
相交所得线段中点的横坐标为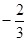 ,求这个双曲线方程。
,求这个双曲线方程。 出发,经过直线
出发,经过直线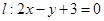 上的一点D反射后,经过点
上的一点D反射后,经过点 .
.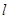 交椭圆C于P、Q两点,以AP、AQ为邻边作平行四边形APRQ,求对角线AR长度的取值范围。
交椭圆C于P、Q两点,以AP、AQ为邻边作平行四边形APRQ,求对角线AR长度的取值范围。 经过点
经过点 ,离心率为
,离心率为 .
.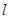 与椭圆交于不同的两点
与椭圆交于不同的两点 、
、 ,且
,且 为锐角(其中
为锐角(其中 为坐标原点),求直线
为坐标原点),求直线 的取值范围.
的取值范围. 的右焦点为
的右焦点为 ,右准线为
,右准线为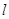 ,点
,点 ,线段
,线段 交
交 于点
于点 ,若
,若 ,则
,则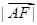 =( )
=( ) b. 2 C.
b. 2 C.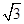 D. 3
D. 3  ,以原点为圆心,椭
,以原点为圆心,椭 圆的短半轴为半径的圆与直线
圆的短半轴为半径的圆与直线 相切.
相切. 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结 交椭圆
交椭圆
 ,证明:直线
,证明:直线 与x轴相交于定点
与x轴相交于定点 ;
; 、
、 两点,求
两点,求 的取值
的取值 的焦点恰好是椭圆
的焦点恰好是椭圆 的右焦点
的右焦点 ,且两条曲线的交点连线也过焦点
,且两条曲线的交点连线也过焦点