题目内容
(本小题满分12分)
已知双曲线的中心在原点,对称轴为坐标轴,焦点在x轴上,两准线间的距离为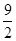 ,并且与直线
,并且与直线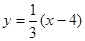 相交所得线段中点的横坐标为
相交所得线段中点的横坐标为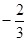 ,求这个双曲线方程。
,求这个双曲线方程。
已知双曲线的中心在原点,对称轴为坐标轴,焦点在x轴上,两准线间的距离为
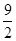 ,并且与直线
,并且与直线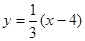 相交所得线段中点的横坐标为
相交所得线段中点的横坐标为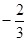 ,求这个双曲线方程。
,求这个双曲线方程。由题意可设所求双曲线方程为:

设直线
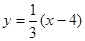 与双曲线相交于
与双曲线相交于 ,
, ,则
,则  (1)-(2)得:
(1)-(2)得:
即

又由线段AB中点的横坐标为
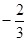 可得,其纵坐标为
可得,其纵坐标为



又





 ,
, ,
,
又
 双曲线两准线间的距离为
双曲线两准线间的距离为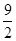









 所求双曲线方程为:
所求双曲线方程为:
略

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案
相关题目
 的焦点
的焦点 为椭圆上的一点,已知
为椭圆上的一点,已知 ,则
,则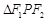 的面积为( )
的面积为( ) 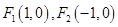 ,过
,过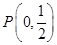 作垂直于
作垂直于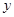 轴的直线被椭圆所截线段长为
轴的直线被椭圆所截线段长为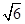 ,过
,过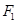 作直线l与椭圆交于A、B两点.
作直线l与椭圆交于A、B两点.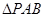 的面积;
的面积;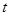 使
使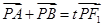 ,若存在,求
,若存在,求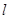 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.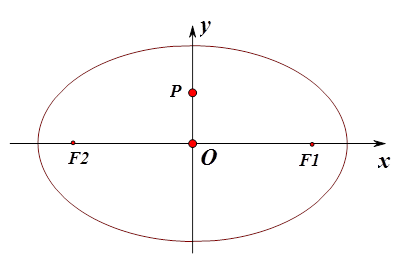
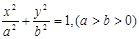 的左、右焦点为
的左、右焦点为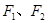 ,其上顶点为
,其上顶点为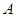 .已知
.已知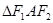 是边长为
是边长为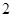 的正三角形.
的正三角形.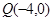 任作一动直线
任作一动直线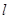 交椭圆C于
交椭圆C于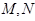 两点,记
两点,记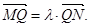 若在线段
若在线段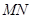 上取一点
上取一点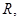 使得
使得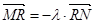 ,试判断当直线
,试判断当直线 是否在某一定直线上运动?若在,请求出该定直线的方程;若不在,请说明理由.
是否在某一定直线上运动?若在,请求出该定直线的方程;若不在,请说明理由.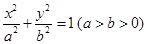 的长半轴长为
的长半轴长为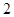 ,且点
,且点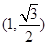 在椭圆上.
在椭圆上.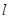 交椭圆于
交椭圆于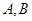 两点,若
两点,若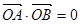 ,求直线
,求直线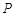 是椭圆
是椭圆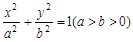 上的一动点,且
上的一动点,且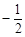 ,则椭圆离心率为 ( )
,则椭圆离心率为 ( )



 的焦点在
的焦点在 轴上,长轴长是短轴长的两倍,则
轴上,长轴长是短轴长的两倍,则 的值为( )
的值为( )

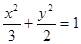 的离心率
的离心率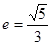 ,长轴长为
,长轴长为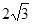 ;②抛物线
;②抛物线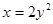 的准线方程为
的准线方程为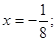 ③双曲线
③双曲线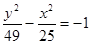 的渐近线方程为
的渐近线方程为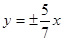 ;④方程
;④方程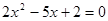 的两根可分别作为椭圆和双曲线的离心率.
的两根可分别作为椭圆和双曲线的离心率. ,
, 是椭圆上关于原点对称的两点,
是椭圆上关于原点对称的两点, 是椭圆上任意一点且直线
是椭圆上任意一点且直线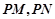 的斜率分别为
的斜率分别为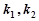 ,
,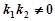 ,则
,则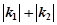 的最小值为
的最小值为 ,则椭圆的离心率为( ).
,则椭圆的离心率为( ).


