题目内容
7.求下列函数的二阶导数:(1)y=(x3+1)3;
(2)y=ex+sinx;
(3)y=xcosx;
(4)y=2x;
(5)y=x2lnx;
(6)y=$\frac{x-1}{x+1}$.
分析 根据导数的公式进行求导即可.
解答 解:(1)y′=3(x3+1)2(3x2)=9(x3+1)2•x2,
y′′=9[(x3+1)2]′•x2+9(x3+1)2•2x
=18(x3+1)•x2+18(x3+1)2=18(x3+1)(x3+x2+1),
(2)y′=ex+cosx,y′′=ex-sinx;
(3)y′=cosx-xsinx,y′′=-cosx-(sinx+xcosx)=-cosx-sinx-xcosx;
(4)y′=2x•ln2,y′′=2x•(ln2)2,
(5)y′=2xlnx+x2•$\frac{1}{x}$=2xlnx+x,y′′=2lnx+2x•$\frac{1}{x}$+1=2lnx+2+2=3+2lnx;
(6)y=$\frac{x-1}{x+1}$=$\frac{x+1-2}{x+1}$=1-$\frac{2}{x+1}$,
则y′=$\frac{2}{(x+1)^{2}}$,y′′=-$\frac{4}{(x+1)^{3}}$.
点评 本题主要考查导数的计算,根据导数的公式是解决本题的关键.考查学生的运算能力.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
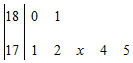 (文科)某校女子篮球队7名运动员身高(单位:厘米)分布的茎叶图如图,已知记录的平均身高为175cm,但记录中有一名运动员身高的末位数字不清晰,如果把其末尾数记为x,那么x的值为2.
(文科)某校女子篮球队7名运动员身高(单位:厘米)分布的茎叶图如图,已知记录的平均身高为175cm,但记录中有一名运动员身高的末位数字不清晰,如果把其末尾数记为x,那么x的值为2.