题目内容
 函数y=Asin(ωx+?)
函数y=Asin(ωx+?) 一段图象如图所示.
一段图象如图所示.
(1)分别求出A,ω,?并确定函数的解析式;
(2)并指出函数y=Asin(ωx+?)的图象是由函数y=sinx的图象怎样变换得到.
解:(1)由函数的图象可知A=2,T=π,所以T=π= ,解得ω=2,
,解得ω=2,
因为函数的图象经过点(- ,0),所以2sin(-
,0),所以2sin(- ×2+φ)=0,
×2+φ)=0,
又|φ|< ,所以φ=
,所以φ= ;
;
所以函数的解析式为:y=2sin(2x+ ).
).
(2)将函数y=sinx的图象向左平移 个单位得到y=sin(x+
个单位得到y=sin(x+ )的图象,
)的图象,
纵坐标不变,横坐标缩小到原来的 倍得到函数y=sin(2x+
倍得到函数y=sin(2x+ )的图象,
)的图象,
接下来横坐标不变纵坐标扩大到原来的2倍得到函数y=2sin(2x+ )的图象.
)的图象.
分析:(1)由图象可求得A=2,T=π,根据周期公式可得ω值,根据图象过点(- ,0)及|φ|<
,0)及|φ|< 可求得φ值;
可求得φ值;
(2)先进行平移变换,再进行伸缩变换即可得到y=Asin(ωx+?)的图象;
点评:本题考查由y=Asin(ωx+?)的部分图象确定其解析式及图象变换问题,属中档题.
 ,解得ω=2,
,解得ω=2,因为函数的图象经过点(-
 ,0),所以2sin(-
,0),所以2sin(- ×2+φ)=0,
×2+φ)=0,又|φ|<
 ,所以φ=
,所以φ= ;
;所以函数的解析式为:y=2sin(2x+
 ).
).(2)将函数y=sinx的图象向左平移
 个单位得到y=sin(x+
个单位得到y=sin(x+ )的图象,
)的图象,纵坐标不变,横坐标缩小到原来的
 倍得到函数y=sin(2x+
倍得到函数y=sin(2x+ )的图象,
)的图象,接下来横坐标不变纵坐标扩大到原来的2倍得到函数y=2sin(2x+
 )的图象.
)的图象.分析:(1)由图象可求得A=2,T=π,根据周期公式可得ω值,根据图象过点(-
 ,0)及|φ|<
,0)及|φ|< 可求得φ值;
可求得φ值;(2)先进行平移变换,再进行伸缩变换即可得到y=Asin(ωx+?)的图象;
点评:本题考查由y=Asin(ωx+?)的部分图象确定其解析式及图象变换问题,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
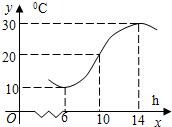 如图所示,某地一天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b,则8时的温度大约为
如图所示,某地一天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b,则8时的温度大约为
 如图,是函数y=Asin(ωx+φ),(-π<φ<π)的图象的一段,O是坐标原点,P是图象的最高点,A点坐标为(5,0),若
如图,是函数y=Asin(ωx+φ),(-π<φ<π)的图象的一段,O是坐标原点,P是图象的最高点,A点坐标为(5,0),若