题目内容
18.如图所示四面体ABCD中,AB、BC、BD两两互相垂直,且AB=BC=2,E是AC中点,异面直线AD与BE所成的角的大小为arccos
18.解法一:如图建立空间直角坐标系.

由题意,有A(0,2,0),C(2,0,0),E(1,1,0),
设D点的坐标为(0,0,z)(z>0),
则![]() ={1,1,0},
={1,1,0},![]() ={0,-2,z}.
={0,-2,z}.
设![]() 与
与![]() 所成的角为θ,
所成的角为θ,
则![]()
![]()
![]() =
=![]()
![]()
![]() cosθ=-2,
cosθ=-2,
且AD与BE所成的角的大小为arccos![]() ,
,
∴cos2θ=![]() =
=![]() ,得z=4,故BD的长度是4.
,得z=4,故BD的长度是4.
又VABCD=![]() AB×BC×BD,因此四面体ABCD的体积是
AB×BC×BD,因此四面体ABCD的体积是![]() .
.
解法二:过A引BE的平行线,交CB的延长线于F,
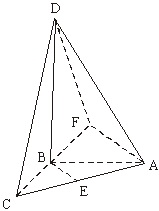
∠DAF是异面直线BE与AD所成的角,
∴∠DAF=arccos![]() .
.
∵E是AC的中点,∴B是CF的中点,AF=2BE=2![]() .
.
又BF,BA分别是DF,DA的射影,且BF=BC=BA,
∴DF=DA.
三角形ADF是等腰三角形,AD=![]()
![]()
![]() =
=![]() ,
,
故BD=![]() =4.
=4.
又VABCD=![]() AB×BC×BD,
AB×BC×BD,
因此四面体ABCD的体积是![]() .
.

练习册系列答案
相关题目
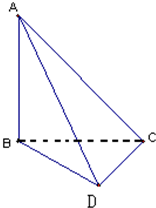 在如图所示的四面体ABCD中,AB、BC、CD两两互相垂直,且BC=CD=1.
在如图所示的四面体ABCD中,AB、BC、CD两两互相垂直,且BC=CD=1.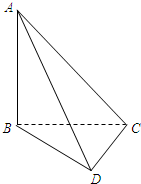 (2009•襄阳模拟)在如图所示的四面体ABCD中,AB、BC、CD两两互相垂直,且BC=CD=1.
(2009•襄阳模拟)在如图所示的四面体ABCD中,AB、BC、CD两两互相垂直,且BC=CD=1. 如图所示,直角梯形ACDE与等腰直角△ABC所在平面互相垂直,F为BC的中点,∠BAC=∠ACD=90°,AE∥CD,DC=AC=2AE=2.
如图所示,直角梯形ACDE与等腰直角△ABC所在平面互相垂直,F为BC的中点,∠BAC=∠ACD=90°,AE∥CD,DC=AC=2AE=2. 如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′两两垂直,E,F,H分别是AC,AB,BC的中点,
如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′两两垂直,E,F,H分别是AC,AB,BC的中点,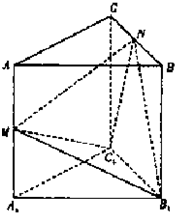 (2010•武汉模拟)如图所示,在正三棱柱ABC-A1B1C1中,底面ABC的边长为2a,侧棱AA1=2a,M、N分别为AA1、BC中点
(2010•武汉模拟)如图所示,在正三棱柱ABC-A1B1C1中,底面ABC的边长为2a,侧棱AA1=2a,M、N分别为AA1、BC中点