题目内容
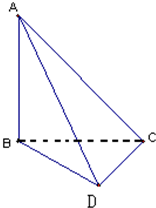 在如图所示的四面体ABCD中,AB、BC、CD两两互相垂直,且BC=CD=1.
在如图所示的四面体ABCD中,AB、BC、CD两两互相垂直,且BC=CD=1.(Ⅰ)求证:平面ACD⊥平面ABC;
(Ⅱ)求二面角C-AB-D的大小;
(Ⅲ)若直线BD与平面ACD所成的角为30°,求线段AB的长度.
分析:(Ⅰ)要证平面ACD⊥平面ABC,只需证明平面ACD内的直线CD,垂直平面ABC内的两条相交直线AB,BC,即可证明CD⊥平面ABC,从而证明平面ACD⊥平面ABC.
(Ⅱ)说明∠CBD是二面角C-AB-D的平面角,解Rt△BCD,求二面角C-AB-D的大小;
(Ⅲ)过点B作BH⊥AC,垂足为H,连接DH.说明∠BDH为BD与平面ACD所成的角,利用直线BD与平面ACD所成的角为30°,解三角形求线段AB的长度.
(Ⅱ)说明∠CBD是二面角C-AB-D的平面角,解Rt△BCD,求二面角C-AB-D的大小;
(Ⅲ)过点B作BH⊥AC,垂足为H,连接DH.说明∠BDH为BD与平面ACD所成的角,利用直线BD与平面ACD所成的角为30°,解三角形求线段AB的长度.
解答: 解:
解:
(Ⅰ)证明:∵CD⊥AB,CD⊥BC,
∴CD⊥平面ABC.(2分)
又∵CD?平面ACD,
∴平面ACD⊥平面ABC.(4分)
(Ⅱ)∵AB⊥BC,AB⊥CD,
∴AB⊥平面BCD∴AB⊥BD.
∴∠CBD是二面角C-AB-D的平面角.(6分)
∵在Rt△BCD中,BC=CD,
∴∠CBD=45°.
∴二面角C-AB-D的大小为45°.(9分)
(Ⅲ)过点B作BH⊥AC,垂足为H,连接DH.∵平面ACD⊥平面ABC,
∴BH⊥平面ACD,
∴∠BDH为BD与平面ACD所成的角.(12分)
∴∠BDH=30°.
在Rt△BHD中,BD=
,
∴BH=
.
又∵在Rt△BHC中,BC=1,
∴∠BCH=45°,
∴在Rt△ABC中,AB=1.(14分)
 解:
解:(Ⅰ)证明:∵CD⊥AB,CD⊥BC,
∴CD⊥平面ABC.(2分)
又∵CD?平面ACD,
∴平面ACD⊥平面ABC.(4分)
(Ⅱ)∵AB⊥BC,AB⊥CD,
∴AB⊥平面BCD∴AB⊥BD.
∴∠CBD是二面角C-AB-D的平面角.(6分)
∵在Rt△BCD中,BC=CD,
∴∠CBD=45°.
∴二面角C-AB-D的大小为45°.(9分)
(Ⅲ)过点B作BH⊥AC,垂足为H,连接DH.∵平面ACD⊥平面ABC,
∴BH⊥平面ACD,
∴∠BDH为BD与平面ACD所成的角.(12分)
∴∠BDH=30°.
在Rt△BHD中,BD=
| 2 |
∴BH=
| ||
| 2 |
又∵在Rt△BHC中,BC=1,
∴∠BCH=45°,
∴在Rt△ABC中,AB=1.(14分)
点评:本题考查平面与平面垂直的判定,直线与平面所成的角,二面角及其度量,考查逻辑思维能力,转化思想,是中档题.

练习册系列答案
相关题目
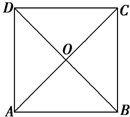 如图所示,在边长为4的正方形纸片ABCD中,AC与BD相交于O,剪去△AOB,将剩余部分沿OC、OD折叠,使OA、OB重合,则以A、(B)、C、D、O为顶点的四面体的体积为
如图所示,在边长为4的正方形纸片ABCD中,AC与BD相交于O,剪去△AOB,将剩余部分沿OC、OD折叠,使OA、OB重合,则以A、(B)、C、D、O为顶点的四面体的体积为 如图所示,在四面体P-ABC中,PA⊥BC,PB⊥AC,BC=2,PB=PC,P-BC-A是60°的二面角.
如图所示,在四面体P-ABC中,PA⊥BC,PB⊥AC,BC=2,PB=PC,P-BC-A是60°的二面角. 菱形ABCD的边长为
菱形ABCD的边长为



 如图所示,在边长为4的正方形纸片ABCD中,AC与BD相交于O,剪去
如图所示,在边长为4的正方形纸片ABCD中,AC与BD相交于O,剪去 ,将剩余部分沿OC、OD折叠,使OA、OB重合,则以A、(B)、C、D、O为顶点的四面体的体积为
,将剩余部分沿OC、OD折叠,使OA、OB重合,则以A、(B)、C、D、O为顶点的四面体的体积为