题目内容
 如图所示,直角梯形ACDE与等腰直角△ABC所在平面互相垂直,F为BC的中点,∠BAC=∠ACD=90°,AE∥CD,DC=AC=2AE=2.
如图所示,直角梯形ACDE与等腰直角△ABC所在平面互相垂直,F为BC的中点,∠BAC=∠ACD=90°,AE∥CD,DC=AC=2AE=2.(1)求证:平面BCD⊥平面ABC;
(2)求证:AF∥平面BDE;
(3)求四面体B-CDE的体积.
分析:(1)证明平面BCD⊥平面ABC,只需证明DC⊥面ABC,利用面ABC⊥面ACDE,CD⊥AC,即可证得;
(2)取BD的中点P,连接EP、FP,则可证四边形AFPE是平行四边形,所以AF∥EP,即可证得AF∥面BDE;
(3)证明BA⊥面ACDE,可得BA就是四面体B-CDE的高,且BA=2,可求S△CDE=3-1=2,即可求得四面体B-CDE的体积.
(2)取BD的中点P,连接EP、FP,则可证四边形AFPE是平行四边形,所以AF∥EP,即可证得AF∥面BDE;
(3)证明BA⊥面ACDE,可得BA就是四面体B-CDE的高,且BA=2,可求S△CDE=3-1=2,即可求得四面体B-CDE的体积.
解答: (1)证明:∵面ABC⊥面ACDE,面ABC∩面ACDE=AC,CD⊥AC,
(1)证明:∵面ABC⊥面ACDE,面ABC∩面ACDE=AC,CD⊥AC,
∴DC⊥面ABC,…(2分)
又∵DC?面BCD,
∴平面BCD⊥平面ABC.…(4分)
(2)解:取BD的中点P,连接EP、FP,则FP∥
DC,FP=
DC
又∵EA∥
DC,EA=
DC
∴EA∥FP,EA=FP…(6分)
∴四边形AFPE是平行四边形,∴AF∥EP,
又∵EP?面BDE且AF?面BDE,∴AF∥面BDE.…(8分)
(3)解:∵BA⊥AC,面ABC∩面ACDE=AC,∴BA⊥面ACDE.
∴BA就是四面体B-CDE的高,且BA=2.…(10分)
∵DC=AC=2AE=2,AE∥DC,
∴S梯形ACDE=
(1+2)×2=3,S△ACE=
×1×2=1,
∴S△CDE=3-1=2,∴VE-CDE=
×2×2=
.…(12分)
 (1)证明:∵面ABC⊥面ACDE,面ABC∩面ACDE=AC,CD⊥AC,
(1)证明:∵面ABC⊥面ACDE,面ABC∩面ACDE=AC,CD⊥AC,∴DC⊥面ABC,…(2分)
又∵DC?面BCD,
∴平面BCD⊥平面ABC.…(4分)
(2)解:取BD的中点P,连接EP、FP,则FP∥
| 1 |
| 2 |
| 1 |
| 2 |
又∵EA∥
| 1 |
| 2 |
| 1 |
| 2 |
∴EA∥FP,EA=FP…(6分)
∴四边形AFPE是平行四边形,∴AF∥EP,
又∵EP?面BDE且AF?面BDE,∴AF∥面BDE.…(8分)
(3)解:∵BA⊥AC,面ABC∩面ACDE=AC,∴BA⊥面ACDE.
∴BA就是四面体B-CDE的高,且BA=2.…(10分)
∵DC=AC=2AE=2,AE∥DC,
∴S梯形ACDE=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△CDE=3-1=2,∴VE-CDE=
| 1 |
| 3 |
| 4 |
| 3 |
点评:本题考查面面垂直,线面平行,考查四面体B-CDE的体积,解题的关键是掌握面面垂直,线面平行的判定方法,属于中档题.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 如图所示,直角梯形ABCD绕边AD所在直线旋转一周形成的面所围成的旋转体是( )
如图所示,直角梯形ABCD绕边AD所在直线旋转一周形成的面所围成的旋转体是( ) (2013•永州一模)如图所示,直角梯形ABCD中,∠A=∠D=90°,AD=2,AB=3,CD=4,P在线段AB上,BP=1,O在CD上,且OP∥AD,将图甲沿OP折叠使得平面OCBP⊥底面ADOP,得到一个多面体(如图乙),M、N分别是AC、OP的中点.
(2013•永州一模)如图所示,直角梯形ABCD中,∠A=∠D=90°,AD=2,AB=3,CD=4,P在线段AB上,BP=1,O在CD上,且OP∥AD,将图甲沿OP折叠使得平面OCBP⊥底面ADOP,得到一个多面体(如图乙),M、N分别是AC、OP的中点.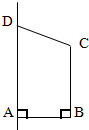
 如图所示,直角梯形ABCD绕边AD所在直线旋转一周形成的面所围成的旋转体是( )
如图所示,直角梯形ABCD绕边AD所在直线旋转一周形成的面所围成的旋转体是( )