题目内容
【题目】已知数列{an}满足0<an<1,且an+1+ ![]() =2an+
=2an+ ![]() (n∈N*).
(n∈N*).
(1)证明:an+1<an;
(2)若a1= ![]() ,设数列{an}的前n项和为Sn , 证明:
,设数列{an}的前n项和为Sn , 证明: ![]() ﹣
﹣ ![]() <Sn<
<Sn< ![]() ﹣2.
﹣2.
【答案】
(1)证明:由an+1+ ![]() =2an+
=2an+ ![]() ,
,
得 ![]() ,即
,即 ![]() ,
,
∴ ![]() ,则
,则 ![]() ,
,
又0<an<1,
∴ ![]() ,即an+1<an
,即an+1<an
(2)证明:由an+1+ ![]() =2an+
=2an+ ![]() ,得
,得 ![]() .
.
∴Sn=a1+a2+…+an= ![]() +…+
+…+ ![]()
= ![]() .
.
又∵an+1+ ![]() =2an+
=2an+ ![]() ,
,
∴ ![]() ,
,
∴ ![]() .
.
由0<an+1<an,可知 ![]() ,
,
即 ![]() ,
,
∴2n ![]() ,
,
∴ ![]() ,
, ![]() ,
,
∵ ![]() .
.
∴ ![]() .
.
∴ ![]() ﹣
﹣ ![]() <Sn<
<Sn< ![]() ﹣2.
﹣2.
【解析】(1)把已知数列递推式变形,可得 ![]() ,结合0<an<1,得到an+1﹣an=
,结合0<an<1,得到an+1﹣an= ![]() <0,即an+1<an;(2)由已知数列递推式得
<0,即an+1<an;(2)由已知数列递推式得 ![]() ,利用累加法得到Sn=
,利用累加法得到Sn= ![]() =an+1+
=an+1+ ![]() .把已知递推式两边平方可得
.把已知递推式两边平方可得 ![]() ,利用放缩法得到
,利用放缩法得到 ![]() ,即2n
,即2n ![]() ,进一步得到
,进一步得到 ![]() ,然后利用不等式的可加性证得
,然后利用不等式的可加性证得 ![]() ﹣
﹣ ![]() <Sn<
<Sn< ![]() ﹣2.
﹣2.
【考点精析】认真审题,首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系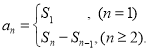 ).
).

练习册系列答案
相关题目