题目内容
某射击小组有甲、乙两名射手，甲的命中率为P1＝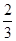
，乙的命中率为P2，在射击比赛活动中每人射击两发子弹则完成一次检测，在一次检测中，若两人命中数相等且都不少于一发，则称该射击小组为“先进和谐组”．
(1)若P2＝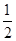
，求该小组在一次检测中荣获“先进和谐组”的概率；
(2)计划在2013年每月进行1次检测，设这12次检测中该小组获得“先进和谐组”的次数为ξ，如果E(ξ)≥5，求P2的取值范围．
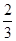，乙的命中率为P2，在射击比赛活动中每人射击两发子弹则完成一次检测，在一次检测中，若两人命中数相等且都不少于一发，则称该射击小组为“先进和谐组”．(1)若P2＝
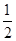，求该小组在一次检测中荣获“先进和谐组”的概率；(2)计划在2013年每月进行1次检测，设这12次检测中该小组获得“先进和谐组”的次数为ξ，如果E(ξ)≥5，求P2的取值范围．
（1）
（2）
≤P2≤1.
（2）≤P2≤1.(1)可得P＝
(
××)＋
＝.
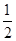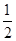(2)该小组在一次检测中荣获“先进和谐组”的概率为P＝[×P2×(1－P2)]＋
＝
P2－
，而ξ～B(12，P)，所以E(ξ)＝12P，由E(ξ)≥5，知(P2－)×12≥5，解得≤P2≤1.
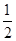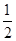(××)＋＝.(2)该小组在一次检测中荣获“先进和谐组”的概率为P＝
[×P2×(1－P2)]＋＝P2－，而ξ～B(12，P)，所以E(ξ)＝12P，由E(ξ)≥5，知(P2－)×12≥5，解得≤P2≤1.
练习册系列答案
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
黄冈360度定制密卷系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
相关题目
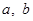的值； 
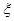，求