题目内容
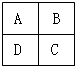 在如图所示的花圃中栽种观赏植物,要求邻块不同色即可.若苗圃中有四种不同颜色的观赏植物供应,试分析可能的栽种方案?
在如图所示的花圃中栽种观赏植物,要求邻块不同色即可.若苗圃中有四种不同颜色的观赏植物供应,试分析可能的栽种方案?分析:(方法一)按色彩种类分:从四种不同颜色里任选两种颜色有
,选取两种颜色
,其中A,C种一种颜色,B,D种另一种颜色,其不同种法有
,故共有
•
种方案;同理:选用三种颜色(A、C同色或B、D同色)的共有
•
种;选用四种颜色(A、B、C、D颜色各不相同)的共有
种,相加即可.
(方法二)按A、C是否同色分:若A、C同色,从四种不同颜色里任选一种颜色有
种,则B从剩下的3种颜色中任取1种可有
中方法,D从与A,C取一种之后剩下的3种颜色中任取一种可有
,于是共有
•
•
=36种;同理A、C不同色,共有
•
•
•
=48种,相加即可.
| C | 2 4 |
| C | 2 2 |
| A | 2 2 |
| C | 2 2 |
| A | 2 4 |
| C | 1 2 |
| A | 3 4 |
| A | 4 4 |
(方法二)按A、C是否同色分:若A、C同色,从四种不同颜色里任选一种颜色有
| A | 1 4 |
| A | 1 3 |
| A | 1 3 |
| A | 1 4 |
| A | 1 3 |
| A | 1 3 |
| A | 1 4 |
| A | 1 3 |
| A | 1 2 |
| A | 1 2 |
解答:解:(方法一)按色彩种类分:
①.选用两种颜色(A、C同色且B、D同色)的共有
•
种,
②.选用三种颜色(A、C同色或B、D同色)的共有
•
种,
③.选用四种颜色(A、B、C、D颜色各不相同)的共有
种,
所以可能共有
•
+
•
+
=84种,
(方法二)按A、C是否同色分:
①.A、C同色,共有
•
•
=36种,
②.A、C不同色,共有
•
•
•
=48种,
所以可能共有36+48=84种.
①.选用两种颜色(A、C同色且B、D同色)的共有
| C | 2 2 |
| A | 2 4 |
②.选用三种颜色(A、C同色或B、D同色)的共有
| C | 1 2 |
| A | 3 4 |
③.选用四种颜色(A、B、C、D颜色各不相同)的共有
| A | 4 4 |
所以可能共有
| C | 2 2 |
| A | 2 4 |
| C | 1 2 |
| A | 3 4 |
| A | 4 4 |
(方法二)按A、C是否同色分:
①.A、C同色,共有
| A | 1 4 |
| A | 1 3 |
| A | 1 3 |
②.A、C不同色,共有
| A | 1 4 |
| A | 1 3 |
| A | 1 2 |
| A | 1 2 |
所以可能共有36+48=84种.
点评:本题考查了分类讨论的思想方法和排列与组合的计算公式及“乘法原理”和“加法原理”,分类讨论要做到不重不漏的原则,要求正确理解排列与组合的计算公式及其意义.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
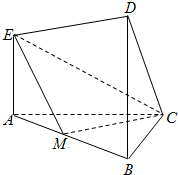 在如图所示的几何体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE,M是AB的中点.
在如图所示的几何体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE,M是AB的中点.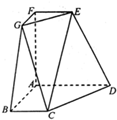 在如图所示的几何体中,四边形ABCD、ADEF、ABGF均为全等的直角梯形,且BC∥AD,AB=AD=2BC.
在如图所示的几何体中,四边形ABCD、ADEF、ABGF均为全等的直角梯形,且BC∥AD,AB=AD=2BC. 对于二次函数y=-2x2+5x
对于二次函数y=-2x2+5x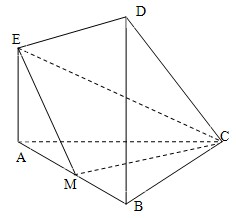 在如图所示的几何体中,三条直线AE,AC,BC两两互相垂直,且AC=BC=BD=2AE,AE∥BD,M是线段AB的中点.
在如图所示的几何体中,三条直线AE,AC,BC两两互相垂直,且AC=BC=BD=2AE,AE∥BD,M是线段AB的中点.