题目内容
 对于二次函数y=-2x2+5x
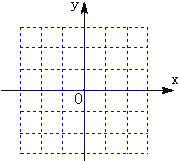
对于二次函数y=-2x2+5x(1)指出图象的开口方向,对称轴方程,顶点坐标;
(2)在如图所示的坐标系中画出该函数的图象;并说明其图象由y=-2x2的图象经过怎样的变换得到的.
(3)写出该函数的定义域、值域、单调区间(不要求证明).
分析:(1)根据二次函数的解析式,求得图象的开口方向,对称轴方程,顶点坐标.
(2)根据二次函数的解析式,画出该函数的图象,根据函数y=-2x2+5x=-(x-
)2+
,结合函数图象的平移变换规律,从而得出结论.
(3)结合函数的图象,可得该函数的定义域、值域、单调区间.
(2)根据二次函数的解析式,画出该函数的图象,根据函数y=-2x2+5x=-(x-
| 5 |
| 4 |
| 25 |
| 8 |
(3)结合函数的图象,可得该函数的定义域、值域、单调区间.
解答: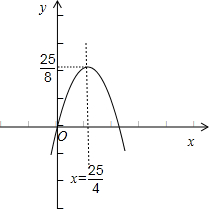 解:(1)由二次函数y=-2x2+5x可得它的图象是开口向上的抛物线,对称轴为x=
解:(1)由二次函数y=-2x2+5x可得它的图象是开口向上的抛物线,对称轴为x=
,
把x=
代入抛物线方程求得y=
,故顶点坐标为(
,
).
(2)在如图所示的坐标系中画出该函数的图象:
由于函数y=-2x2+5x=-(x-
)2+
,故把数y=-2x2 的图象向右平移
个单位,
再把所得图象向上平移
个单位即可得到数y=-2x2+5x 的图象.
(3)该函数的定义域为 R,值域为(-∞,
],单调增区间为(-∞,
],
单调减区间为(
,+∞).
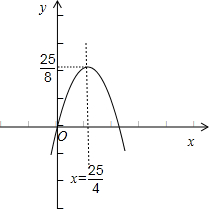 解:(1)由二次函数y=-2x2+5x可得它的图象是开口向上的抛物线,对称轴为x=
解:(1)由二次函数y=-2x2+5x可得它的图象是开口向上的抛物线,对称轴为x=| 5 |
| 4 |
把x=
| 5 |
| 4 |
| 25 |
| 8 |
| 5 |
| 4 |
| 25 |
| 8 |
(2)在如图所示的坐标系中画出该函数的图象:
由于函数y=-2x2+5x=-(x-
| 5 |
| 4 |
| 25 |
| 8 |
| 5 |
| 4 |
再把所得图象向上平移
| 25 |
| 8 |
(3)该函数的定义域为 R,值域为(-∞,
| 25 |
| 8 |
| 25 |
| 4 |
单调减区间为(
| 25 |
| 4 |
点评:本题主要考查二次函数的图象和性质,函数图象的平移变换规律的应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目