题目内容
设函数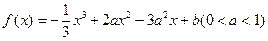
（1）求函数f(x)的单调区间，并求函数f(x)的极大值和极小值；
（2）当x∈[a+1, a+2]时，不等
，求a的取值范围.
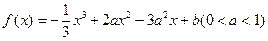
（1）求函数f(x)的单调区间，并求函数f(x)的极大值和极小值；
（2）当x∈[a+1, a+2]时，不等
，求a的取值范围.（1）函数f(x)的极大值为b，极小值为－
a3+b
（2）a的取值范围是
a3+b （2）a的取值范围是
（1）∵f′(x)=－x2+4ax－3a2=－(x－3a)(x－a),由f′(x)>0得：a<x<3a
由f′(x)<0得，x<a或x>3a，
则函数f(x)的单调递增区间为（a, 3a），单调递减区间为（－∞，a）和（3a，+∞）
列表如下：
∴函数f(x)的极大值为b，极小值为－a3+b …………………………7分
（2）
上单调递
减，因此
∵不等式|f′(x)|≤a恒成立，
∴
即a的取值范围是
由f′(x)<0得，x<a或x>3a，
则函数f(x)的单调递增区间为（a, 3a），单调递减区间为（－∞，a）和（3a，+∞）
列表如下：
| x | (－∞，a) | a | (a, 3a) | 3a | (3a,+ ∞) |
| f′(x) | — | 0 | + | 0 | — |
| f(x) |  | －a3+b |  | b |  |
a3+b …………………………7分（2）
上单调递减，因此
∵不等式|f′(x)|≤a恒成立，
∴
即a的取值范围是
练习册系列答案
相关题目
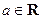，若函数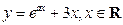
有大于零的极值点，则
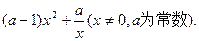
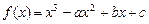的图象为曲线E.
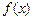可以在
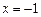和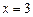
时取得极值，并求此时a,b的值；
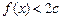在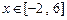
恒成立，求c的取值范围.
= 
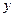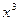－12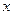
+16在 [－3,3]上的最大值、最小值分别是（ ）
，
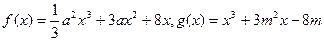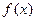在x=1处的切线斜率的取值范围；
，总存在
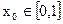，使得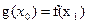
成立？若存在，求出实数m的取值范围；若不存在，说明理由．