题目内容
(本小题满分12分)
设函数f (x)=ln(x+a)+x2.
(Ⅰ)若当x=1时,f (x)取得极值,求a的值,并讨论f (x)的单调性;
(Ⅱ)若f (x)存在极值,求a的取值范围,并证明所有极值之和大于ln.
设函数f (x)=ln(x+a)+x2.
(Ⅰ)若当x=1时,f (x)取得极值,求a的值,并讨论f (x)的单调性;
(Ⅱ)若f (x)存在极值,求a的取值范围,并证明所有极值之和大于ln.
(Ⅰ) ;
; 分别在区间
分别在区间 单调递增,在区间
单调递增,在区间 单调递减.
单调递减.
(Ⅱ) ,证明见解析
,证明见解析
 ;
; 分别在区间
分别在区间 单调递增,在区间
单调递增,在区间 单调递减.
单调递减.(Ⅱ)
 ,证明见解析
,证明见解析(Ⅰ)
 ,依题意有
,依题意有 ,故
,故 .
.从而
 .
. 的定义域为
的定义域为 ,
,当
 时,
时, ;当
;当 时,
时, ;
;当
 时,
时, .
. 分别在区间
分别在区间 单调递增,在区间
单调递增,在区间 单调递减.
单调递减.(Ⅱ)
 的定义域为
的定义域为 ,
, .
.方程
 的判别式
的判别式 .
.(ⅰ)若
 ,即
,即 ,在
,在 的定义域内
的定义域内 ,故
,故 无极值.
无极值.(ⅱ)若
 ,则
,则 或
或 .
.若
 ,
, ,
, .
.当
 时,
时, ,
,当
 时,
时, ,所以
,所以 无极值.
无极值.若
 ,
, ,
, ,
, 也无极值.
也无极值.(ⅲ)若
 ,即
,即 或
或 ,则
,则 有两个不同的实根
有两个不同的实根 ,
, .
.当
 时,
时, ,从而
,从而 有
有 的定义域内没有零点,故
的定义域内没有零点,故 无极值.
无极值.当
 时,
时, ,
, ,
, 在
在 的定义域内有两个不同的零点,由根值判别方法知
的定义域内有两个不同的零点,由根值判别方法知 在
在 取得极值.
取得极值.综上,
 存在极值时,
存在极值时, 的取值范围为
的取值范围为 .
. 的极值之和为
的极值之和为 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
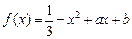 的图像在点P(0,f(0))处的切线方程为
的图像在点P(0,f(0))处的切线方程为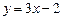 .
.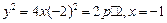
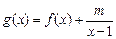 是
是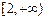 上的增函数.
上的增函数.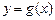 围成两个封闭图形,则这两个封闭图形的面积总相等?若存在,求出点Q的坐标;若不存在,说明理由.
围成两个封闭图形,则这两个封闭图形的面积总相等?若存在,求出点Q的坐标;若不存在,说明理由.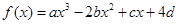 (
(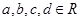 )的图象关于原点对称,且
)的图象关于原点对称,且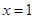 时,
时,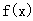 取极小值
取极小值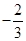 ,
,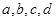 的值;
的值; 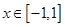 时,图象上是否存在两点,使得过此两点处的切线互相垂直?试证明你的结论。
时,图象上是否存在两点,使得过此两点处的切线互相垂直?试证明你的结论。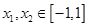 ,求证:
,求证: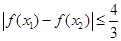 。
。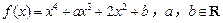 .
.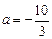 时,讨论函数
时,讨论函数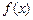 的单调性;
的单调性;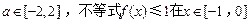 上恒成立,求b的取值范围.
上恒成立,求b的取值范围.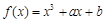 .
.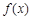 在x = 0处取得极值为 – 2,求a、b的值;
在x = 0处取得极值为 – 2,求a、b的值;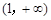 上是增函数,求实数a的取值范围.
上是增函数,求实数a的取值范围.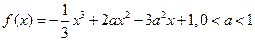 。
。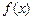 的极大值;
的极大值;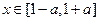 时,恒有
时,恒有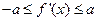 成立(其中
成立(其中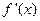 是函数
是函数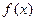 的导函数),试确定实数
的导函数),试确定实数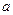 的取值范围。
的取值范围。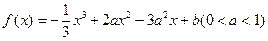
 ,求a的取值范围.
,求a的取值范围.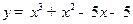 的单调增区间是___________________________。
的单调增区间是___________________________。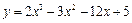 在区间[0,3]上的最大值与最小值分别是( )
在区间[0,3]上的最大值与最小值分别是( )