题目内容
2.在△ABC中,已知a=4,B=60°,A=30°,解三角形.分析 由三角形的内角和定理求得C,然后直接利用正弦定理得答案.
解答 解:∵B=60°,A=30°,
∴C=180°-60°-30°=90°,
由正弦定理得b=4$\sqrt{3}$,c=8,
点评 本题考查了解三角形,考查了正弦定理的应用,是基础题.

练习册系列答案
相关题目
17.在等比数列{an}中,a5=2,a7=8,则a6等于( )
| A. | 4 | B. | 5 | C. | -4 | D. | ±4 |
7.在空间直角坐标系中,已知点Q(-3,1,4),则点Q关于xOz面的对称点的坐标为( )
| A. | (3,-1,-4) | B. | (-3,-1,-4) | C. | (3,1,4) | D. | (-3,-1,4) |
14.已知抛物线x2=4py(p>0)的焦点F,直线y=x+2与该抛物线交于A,B两点,M是线段AB的中点,过M作x轴的垂线,垂足为N,若$\overrightarrow{AF}$•$\overrightarrow{BF}$+($\overrightarrow{AF}$+$\overrightarrow{BF}$)•$\overrightarrow{FN}$=-1-5p2,则p的值为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
11.已知a=30.4,b=0.43,c=log0.43,则( )
| A. | b<a<c | B. | c<a<b | C. | c<b<a | D. | a<c<b |
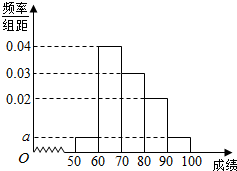 某校200位学生期末考试物理成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100].
某校200位学生期末考试物理成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100].