题目内容
在△ABC中,角A,B,C的对边分别为a,b,c,且满足(2c-a)cosB-bcosA=0.
(1)若b=2,求△ABC的面积的最大值;
(2)求
sinA+sin(C-
)的取值范围.
(1)若b=2,求△ABC的面积的最大值;
(2)求
| 3 |
| π |
| 6 |
考点:正弦定理
专题:计算题,三角函数的图像与性质,解三角形
分析:利用正弦定理化简已知条件,根据三角形的内角和定理及诱导公式化简,由sinC不为0,得到cosB的值,由B的范围,利用特殊角的三角函数值即可得到B的度数,
(1)根据余弦定理,由b,cosB和基本不等式,求出ac的最大值,然后利用三角形的面积公式,即可得到最大值;
(2)由求出的B的度数,根据三角形的内角和定理得到A+C的度数,用A表示出C,代入已知的等式,利用诱导公式及两角和的正弦函数公式化为一个角的正弦函数,根据A的范围求出这个角的范围,由正弦函数的值域即可得到所求式子的取值范围.
(1)根据余弦定理,由b,cosB和基本不等式,求出ac的最大值,然后利用三角形的面积公式,即可得到最大值;
(2)由求出的B的度数,根据三角形的内角和定理得到A+C的度数,用A表示出C,代入已知的等式,利用诱导公式及两角和的正弦函数公式化为一个角的正弦函数,根据A的范围求出这个角的范围,由正弦函数的值域即可得到所求式子的取值范围.
解答:
解:由已知及正弦定理得:(2sinC-sinA)cosB-sinBcosA=0,
即2sinCcosB-sin(A+B)=0,
在△ABC中,由sin(A+B)=sinC
故sinC(2cosB-1)=0,
由B,C∈(0,π),则2cosB-1=0,
所以B=60°;
(1)由b2=a2+c2-2accos60°≥2ac-ac=ac,
即ac≤4,当且仅当a=c=2,取得最大值4.
所以△ABC的面积S=
acsinB≤
×4×
=
,
即有面积的最大值为
;
(2)因为
sinA+sin(C-
)=
sinA+sin(
-A)
=
sinA+cosA=2sin(A+
)
又A∈(0,
),即有A+
∈(
,
),
即有sin(A+
)∈(
,1],
则
sinA+sin(C-
)=2sin(A+
)∈(1,2].
即2sinCcosB-sin(A+B)=0,
在△ABC中,由sin(A+B)=sinC
故sinC(2cosB-1)=0,
由B,C∈(0,π),则2cosB-1=0,
所以B=60°;
(1)由b2=a2+c2-2accos60°≥2ac-ac=ac,
即ac≤4,当且仅当a=c=2,取得最大值4.
所以△ABC的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
即有面积的最大值为
| 3 |
(2)因为
| 3 |
| π |
| 6 |
| 3 |
| π |
| 2 |
=
| 3 |
| π |
| 6 |
又A∈(0,
| 2π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
即有sin(A+
| π |
| 6 |
| 1 |
| 2 |
则
| 3 |
| π |
| 6 |
| π |
| 6 |
点评:此题考查学生灵活运用正弦定理及诱导公式化简求值,灵活运用三角形的面积公式及两角和的正弦函数公式化简求值,掌握正弦函数的值域,是一道中档题.

练习册系列答案
相关题目
设点O是△ABC的外心,AB=13,AC=12,则
•
为( )
| BC |
| AO |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知θ是三角形的一个内角,且sinθ+cosθ=
,则x2sinθ-y2cosθ=1表示( )
| 1 |
| 2 |
| A、焦点在x轴上的椭圆 |
| B、焦点在x轴上的双曲线 |
| C、焦点在y轴上的椭圆 |
| D、焦点在y轴上的双曲线 |
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象与直线y=b (0<b<A)的三个相邻交点的横坐标分别是2,4,8,则f(x)的单调递增区间是( )
| A、[6kπ,6kπ+3],k∈Z |
| B、[6k-3,6k],k∈Z |
| C、[6k,6k+3],k∈Z |
| D、无法确定 |
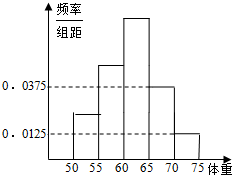 为了了解高三学生的身体状况.抽取了部分男生的体重,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为12,则抽取的男生人数是( )
为了了解高三学生的身体状况.抽取了部分男生的体重,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为12,则抽取的男生人数是( )