题目内容
函数f(θ)=sin2θ+2(sinθ+cosθ)+3(θ∈R)的值域为 .
分析:利用倍角公式和换元法,可将求函数f(θ)=sin2θ+2(sinθ+cosθ)+3(θ∈R)的值域,转化为求二次函数在定区间上的值域问题,进而利用二次函数的图象和性质进行解答.
解答:解:f(θ)=sin2θ+2(sinθ+cosθ)+3
=sin2θ+cos2θ+2sinθ•cosθ+2(sinθ+cosθ)+2
=(sinθ+cosθ)2+2(sinθ+cosθ)+2
令t=sinθ+cosθ=
sin(θ+
),则t∈[-
,
]
则y=f(θ)=t2+2t+2,t∈[-
,
]
∵y=t2+2t+2的图象是开口朝上,且以直线t=-1为对称轴的抛物线
故当t=-1时,函数y=f(θ)=t2+2t+2取最小值1;
当t=
时,函数y=f(θ)=t2+2t+2取最大值4+2
;
故函数的值域为[1,4+2
]
故答案为:[1,4+2
]
=sin2θ+cos2θ+2sinθ•cosθ+2(sinθ+cosθ)+2
=(sinθ+cosθ)2+2(sinθ+cosθ)+2
令t=sinθ+cosθ=
| 2 |
| π |
| 4 |
| 2 |
| 2 |
则y=f(θ)=t2+2t+2,t∈[-
| 2 |
| 2 |
∵y=t2+2t+2的图象是开口朝上,且以直线t=-1为对称轴的抛物线
故当t=-1时,函数y=f(θ)=t2+2t+2取最小值1;
当t=
| 2 |
| 2 |
故函数的值域为[1,4+2
| 2 |
故答案为:[1,4+2
| 2 |
点评:本题考查的知识点是函数的值域,和差角公式,二倍角公式,是二次函数和三角函数的综合应用,难度中档.

练习册系列答案
相关题目
已知函数f(x)=sin(πx-
)-1,则下列命题正确的是( )
| π |
| 2 |
| A、f(x)是周期为1的奇函数 |
| B、f(x)是周期为2的偶函数 |
| C、f(x)是周期为1的非奇非偶函数 |
| D、f(x)是周期为2的非奇非偶函数 |
 已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<π)的图象如图所示.
已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<π)的图象如图所示.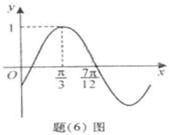 已知函数f(x)=sin(ωx+φ)(ω>0,
已知函数f(x)=sin(ωx+φ)(ω>0,