Question

已知动圆过定点(,0),且与直线x=-相切,其中p＞0.

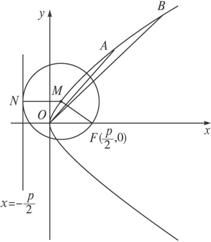
    (1)求动圆圆心P的轨迹C的方程;

    (2)设A、B是轨迹C上异于原点O的两个不同点,直线OA和OB的倾斜角分别为α和β,当α、β变化且α+β为定值θ(0＜θ＜π)时,证明直线AB恒过定点,并求出该定点的坐标.

Answer 1

思路分析:(1)动点P的轨迹满足抛物线定义易求;

(2)紧紧抓住θ为定值,tanθ=tan(α+β)=,而tanα、tanβ都可用y₁,y₂,x₁,x₂表达,可结合韦达定理.但上述变形需有前提θ≠.否则,先行验证.

(1)解:作图易知,动圆圆心P到定点(,0)与到定直线x=-距离相等.

∴动点P的轨迹是抛物线,方程为y²=2px.

(2)证明:设A(x₁,y₁)、B(x₂,y₂),则x₁=,x₂=(x₁≠x₂,否则α+β=π,且x₁·x₂≠0)

设BA:y=kx+b,代入抛物线C的方程,则ky²-2py+2pb=0.

由韦达定理:y₁+y₂=,y₁y₂=.             (*)

①当θ=α+β=时,tanα·tanβ=1,

∴=1.∴0=x₁x₂-y₁y₂=-y₁y₂,

解得y₁y₂=4p²,结合(*)式得b=2pk.

∴AB:y=kx+2pk,

即y=k(x+2p),

∴直线恒过定点(-2p,0).

②当θ≠时,tanθ=.

把(*)式代入整理,化简得

tanθ=,∴b=+2pk.

此时AB:y=kx++2pk,

即y-=k(x+2p),

∴直线恒过定点(-2p,).

总之,当θ=时,直线AB恒过定点?(-2p,0),当θ≠且θ∈(0,π)时,直线AB恒过定点(-2p,).