题目内容
14.经过点P(-3,0),Q(0,-2)的椭圆的标准方程是( )| A. | $\frac{x^2}{9}+\frac{y^2}{4}=1$ | B. | $\frac{x^2}{4}+\frac{y^2}{9}=1$ | C. | $\frac{x^2}{3}+\frac{y^2}{2}=1$ | D. | $\frac{x^2}{2}+\frac{y^2}{3}=1$ |
分析 根据经过点P(-3,0),Q(0,-2),表示出长轴,短轴长,然后写出椭圆的标准方程即可.
解答 解:∵经过点P(-3,0),Q(0,-2)
∴a=3,b=2
∴椭圆的标准方程为$\frac{x^2}{9}+\frac{y^2}{4}=1$
故选:A.
点评 此题考查学生会利用待定系数法求椭圆的标准方程,是一道基础题.学生做题时应注意椭圆的焦点所在位置.

练习册系列答案
相关题目
2.函数y=2cosx(sinx+cosx)的最大值为( )
| A. | 2 | B. | $\sqrt{2}$-1 | C. | $\sqrt{2}$ | D. | $\sqrt{2}$+1 |
4.已知向量$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(0,-2),则与向量$\overrightarrow{b}$-$\overrightarrow{a}$垂直的单位向量为( )
| A. | (-2,1)或(2,-1) | B. | (-1,2)或(1,-2) | ||
| C. | (-$\frac{\sqrt{5}}{5}$,$\frac{2\sqrt{5}}{5}$)或($\frac{\sqrt{5}}{5}$,-$\frac{2\sqrt{5}}{5}$) | D. | (-$\frac{2\sqrt{5}}{5}$,$\frac{\sqrt{5}}{5}$)或($\frac{2\sqrt{5}}{5}$,-$\frac{\sqrt{5}}{5}$) |
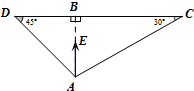 将两个直角三角形如图拼在一起,当E点在线段AB上移动时,若$\overrightarrow{AE}=λ\overrightarrow{AC}+μ\overrightarrow{AD}$,当λ取最大值时,λ-μ的值是$\sqrt{3}$-2.
将两个直角三角形如图拼在一起,当E点在线段AB上移动时,若$\overrightarrow{AE}=λ\overrightarrow{AC}+μ\overrightarrow{AD}$,当λ取最大值时,λ-μ的值是$\sqrt{3}$-2.