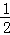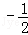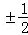题目内容
设数列 的前
的前 项和为
项和为 ,
,
已知 ,
, ,
, ,
, 是数列
是数列 的前
的前 项和.
项和.
(1)求数列 的通项公式;(2)求
的通项公式;(2)求 ;
;
(3)求满足 的最大正整数
的最大正整数 的值.
的值.
 的前
的前 项和为
项和为 ,
,已知
 ,
, ,
, ,
, 是数列
是数列 的前
的前 项和.
项和.(1)求数列
 的通项公式;(2)求
的通项公式;(2)求 ;
;(3)求满足
 的最大正整数
的最大正整数 的值.
的值.(1) ;(2)
;(2) ;(3)1
;(3)1
 ;(2)
;(2) ;(3)1
;(3)1试题分析:(1)由
 可构造
可构造 的递推式,
的递推式, 从而得到通项的递推式,即可得到通项公式.
从而得到通项的递推式,即可得到通项公式.(2)由(1)以及数列
 ,可得到数列
,可得到数列 为等差数列,即可求出通项公式,再根据等差数列的前n和公式可得及轮.
为等差数列,即可求出通项公式,再根据等差数列的前n和公式可得及轮.(3)由(2)可得
 .所以由
.所以由 通项即
通项即 .即可求得
.即可求得 的值
的值 ,再解不等式即可得结论.
,再解不等式即可得结论.(1) 解:∵当
 时,
时, ,
, ∴

∴

∵
 ,
, ,
, ∴

∴数列
 是以
是以 为首项,公比为
为首项,公比为 的等比数列.
的等比数列. ∴

(2) 解:由(1)得:
 ,
, ∴




(3)解:





令
 >2013/2014,解得:n<1007/1006
>2013/2014,解得:n<1007/1006 故满足条件的最大正整数
 的值为1
的值为1 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
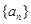 的前n项和为
的前n项和为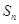 ,存在常数A,B,C,使得
,存在常数A,B,C,使得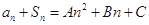 对任意正整数n都成立.
对任意正整数n都成立.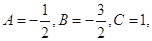 设
设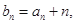 数列
数列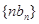 的前n项和为
的前n项和为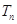 ,求
,求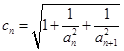 数列
数列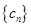 的前2014项和为P,求不超过P的最大整数的值.
的前2014项和为P,求不超过P的最大整数的值.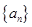 的前
的前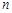 项和
项和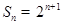 ,数列
,数列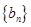 满足
满足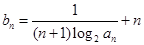 .
.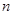 项和
项和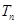 .
. 是公差不为0的等差数列
是公差不为0的等差数列 的前
的前 项和,已知
项和,已知 ,且
,且 成等比数列;
成等比数列; 的通项公式;
的通项公式; 的前
的前 项和。
项和。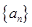 中,
中, ,且有
,且有 .
. 所有可能的值;
所有可能的值; ,都有
,都有 成立?若有,请写出这个数列的前6项,若没有,说明理由;
成立?若有,请写出这个数列的前6项,若没有,说明理由;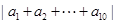 的最小值.
的最小值. ,α=a+
,α=a+ ,β=b+
,β=b+ ,则α+β的最小值为
,则α+β的最小值为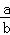 的值是( )
的值是( )