题目内容
数列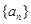 的前n项和为
的前n项和为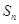 ,存在常数A,B,C,使得
,存在常数A,B,C,使得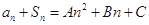 对任意正整数n都成立.
对任意正整数n都成立.
⑴若数列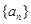 为等差数列,求证:3A B+C=0;
为等差数列,求证:3A B+C=0;
⑵若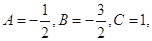 设
设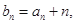 数列
数列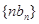 的前n项和为
的前n项和为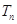 ,求
,求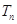 ;
;
⑶若C=0,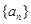 是首项为1的等差数列,设
是首项为1的等差数列,设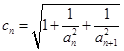 数列
数列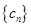 的前2014项和为P,求不超过P的最大整数的值.
的前2014项和为P,求不超过P的最大整数的值.
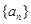 的前n项和为
的前n项和为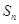 ,存在常数A,B,C,使得
,存在常数A,B,C,使得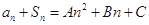 对任意正整数n都成立.
对任意正整数n都成立.⑴若数列
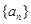 为等差数列,求证:3A B+C=0;
为等差数列,求证:3A B+C=0;⑵若
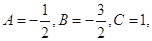 设
设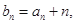 数列
数列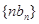 的前n项和为
的前n项和为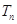 ,求
,求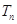 ;
;⑶若C=0,
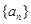 是首项为1的等差数列,设
是首项为1的等差数列,设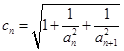 数列
数列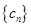 的前2014项和为P,求不超过P的最大整数的值.
的前2014项和为P,求不超过P的最大整数的值.(1)详见解析,(2)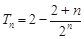 ,(3)2014.
,(3)2014.
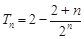 ,(3)2014.
,(3)2014.试题分析:(1)研究特殊数列问题,一般从其特征量出发. 因为
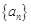 为等差数列,设公差为
为等差数列,设公差为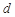 ,由
,由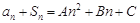 ,得
,得 ,根据恒等式对应项系数相等得:
,根据恒等式对应项系数相等得: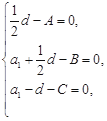 所以
所以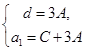 代入
代入 得:
得: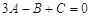 . (2)本题实质为求通项. 因为
. (2)本题实质为求通项. 因为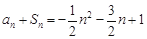 ,所以
,所以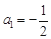 ,当
,当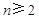 时,
时,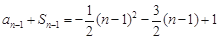 , 所以
, 所以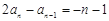 即
即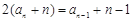 即
即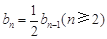 ,而
,而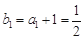 ,所以数列
,所以数列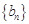 是首项为
是首项为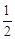 ,公比为
,公比为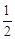 的等比数列,所以
的等比数列,所以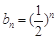 .由错位相减法得
.由错位相减法得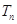 ,(3)因为
,(3)因为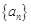 是首项为
是首项为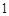 的等差数列,由⑴知,公差
的等差数列,由⑴知,公差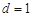 ,所以
,所以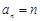 .化简数列
.化简数列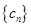 通项
通项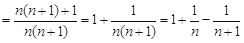 ,再由裂项相消法得
,再由裂项相消法得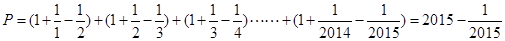 ,所以不超过
,所以不超过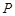 的最大整数为2014.
的最大整数为2014.解 ⑴因为
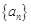 为等差数列,设公差为
为等差数列,设公差为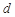 ,由
,由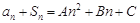 ,
, 得
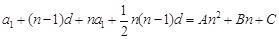 , 2分
, 2分对任意正整数
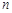 所以
所以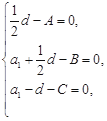 4分
4分所以
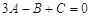 . 6分
. 6分⑵ 因为
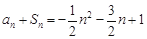 ,所以
,所以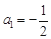 ,
, 当
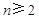 时,
时,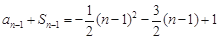 ,
, 所以
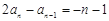 即
即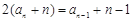 即
即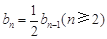 ,而
,而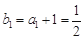 ,
, 所以数列
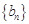 是首项为
是首项为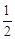 ,公比为
,公比为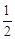 的等比数列,所以
的等比数列,所以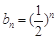 . 9分
. 9分 于是
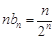 .所以
.所以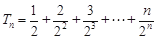 ①,
①,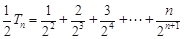 ,②
,②得
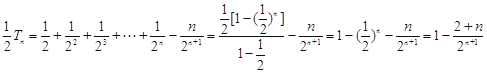 .
. 所以
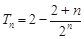 . 12分
. 12分⑶ 因为
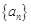 是首项为
是首项为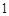 的等差数列,由⑴知,公差
的等差数列,由⑴知,公差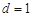 ,所以
,所以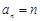 .
. 而
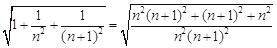
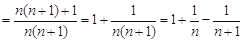 , 14分
, 14分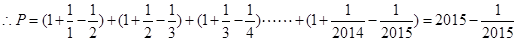 所以不超过
所以不超过 的最大整数为2014. 16分
的最大整数为2014. 16分
练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
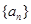 的首项
的首项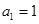 ,公差
,公差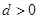 ,且第
,且第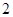 项、第
项、第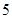 项、第
项、第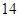 项分别是等比数列
项分别是等比数列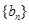 的第
的第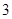 项、第
项、第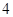 项.
项.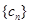 对任意
对任意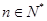 ,均有
,均有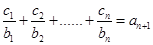 成立.
成立.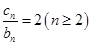 ; ②求
; ②求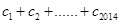 .
.
 是等差数列,首项
是等差数列,首项
 ,
, ,则使前n项和
,则使前n项和 成立的最大正整数n是( )
成立的最大正整数n是( ) ,定义
,定义 .
. ,则
,则 ;
; ,则
,则 的取值范围是 .
的取值范围是 . 的前
的前 项和为
项和为 ,
, ,
, ,
, ,
, 是数列
是数列 的前
的前 的最大正整数
的最大正整数 的前
的前 项为
项为 、
、 、
、 、
、 、
、 ,据此可写出数列
,据此可写出数列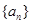 满足:若x是数列
满足:若x是数列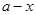 也是数列
也是数列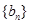 是“兑换数列”,则数列
是“兑换数列”,则数列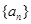 的前
的前 项和
项和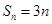 ,则此数列的通项公式为____________________.
,则此数列的通项公式为____________________.