题目内容

已知C：
x2
a2
+
y2
b2
=1(a＞b＞0)椭圆具有性质：若M，N是椭圆上关于原点O对称的两点，点P是椭圆上任意一点，当直线PM，PN的斜率都存在，并记为kPM，kPN时，那么kPM与kPN之积是与点P的位置无关的定值，试写出双曲线
x2
a2
-
y2
b2
=1具有类似特性的性质并加以证明．
分析：设出M和N的坐标，代入双曲线的方程，设点P的坐标，进而表示出PM，PN的斜率，求得两斜率之积．把点P的坐标代入双曲线方程表示出y和n，代入PM，PN斜率之积得表达式求得结果为常数，故可推断出kPM•kPN与点P的位置无关的定值．
解答：解：可以通过横向类比得：若M，N是上述双曲线上关于原点O对称的两点，
点P是双曲线上任意一点，当直线PM，PN的斜率都存在，并记为kPM，kPN时，
那么kPM与kPN之积是与点P的位置无关的定值．
下面给出严格的证明：
设点M（m，n），则N（-m，-n），其中
m2
a2
-
n2
b2
=1，又设点P的坐标
为P（x，y），则kPM=
y-n
x-m
，kPN=
y+n
x+m
，kPM•kPN=
y2-n2
x2-m2
，
注意到
m2
a2
-
n2
b2
=1，点P（x，y）在双曲线
x2
a2
-
y2
b2
=1上，
故y2=b2(
x2
a2
-1)，n2=b2(
m2
a2
-1)，
代入kPM•kPN=
y2-n2
x2-m2
可得：kPM•kPN=
b2
a2
(x2-m2)
x2-m2
=
b2
a2
（常数），
即kPM•kPN与点P的位置无关的定值
点评：本题主要考查了椭圆的应用，考查了学生综合分析问题和解决问题的能力．
练习册系列答案
相关题目
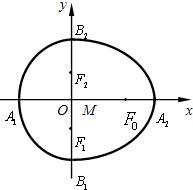精英家教网已知半椭圆
x2
a2
+
y2
b2
=1(x≥0)与半椭圆
y2
b2
+
x2
c2
=1(x≤0)组成的曲线称为“果圆”，其中a2=b2+c2，a＞0，b＞c＞0．如图，设点F0，F1，F2是相应椭圆的焦点，A1，A2和B1，B2是“果圆”与x，y轴的交点，
（1）若三角形F0F1F2是边长为1的等边三角形，求“果圆”的方程；
（2）若|A1A|＞|B1B|，求
b
a
的取值范围；
（3）一条直线与果圆交于两点，两点的连线段称为果圆的弦．是否存在实数k，使得斜率为k的直线交果圆于两点，得到的弦的中点的轨迹方程落在某个椭圆上？若存在，求出所有k的值；若不存在，说明理由．
已知直线l：y=x+1与曲线C：
x2
a2
+
y2
b2
=1(a＞0，b＞0)交于不同的两点A，B，O为坐标原点．
（Ⅰ）若|OA|=|OB|，求证：曲线C是一个圆；
（Ⅱ）若OA⊥OB，当a＞b且a∈[
6
2
，
10
2
]时，求曲线C的离心率e的取值范围．
已知直线L：y=x+1与曲线C：
x2
a2
+
y2
b2
=1(a＞1，b＞0)交于不同的两点A、B，O为坐标原点．
（1）若|OA|=|OB|，试探究在曲线C上仅存在几个点到直线L的距离恰为a-
2
2
？并说明理由；
（2）若OA⊥OB，且a＞b，a∈[
6
2
，
10
2
]，试求曲线C的离心率e的取值范围．
（2013•临沂三模）已知直线l：y=x+
6
，圆O：x2+y2=5，椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的离心率e=
3
3
，直线l被圆O截得的弦长与椭圆的短轴长相等．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过椭圆右焦点F的直线l与椭圆C交于A，B两点．
（1）若
AF
=2
FB
求直线l的方程；
（2）若动点P满足
OP
=
OA
+
OB
，问动点P的轨迹能否与椭圆C存在公共点？若存在，求出点P的坐标；若不存在，请说明理由．
（2007•武汉模拟）已知直线l：y=2x-
3
与椭圆C：
x2
a2
+y2=1 （a＞1）交于P、Q两点，以PQ为直径的圆过椭圆C的右顶点A．
（1）设PQ中点M（x0，y0），求证：x0＜
3
2
（2）求椭圆C的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网