题目内容
(本题满分13分)
设函数 .
.
(Ⅰ)求 的最小值
的最小值 ;
;
(Ⅱ)若 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
【答案】
(Ⅰ)
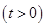 .(Ⅱ)
.(Ⅱ) 。
。
【解析】
试题分析:(Ⅰ) ,
,
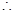 当
当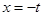 时,
时, 取最小值
取最小值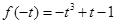 ,
,
即
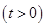 .---------------------------------------------------(4分)
.---------------------------------------------------(4分)
(Ⅱ)令 ,
,
由 得
得 ,
,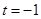 (不合题意,舍去).
(不合题意,舍去).
当 变化时
变化时 ,
, 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
递增 |
极大值 |
递减 |
 在
在 内有最大值
内有最大值 .---------------------------------------(8分)
.---------------------------------------(8分)
 在
在 内恒成立等价于
内恒成立等价于 在
在 内恒成立,
内恒成立,
即等价于 ,
,
所以 的取值范围为
的取值范围为 .--------------------------------------------------(13分)
.--------------------------------------------------(13分)
考点:二次函数的性质;恒成立问题;函数的最值。
点评:解决恒成立问题常用变量分离法,变量分离法主要通过两个基本思想解决恒成立问题, 思路1: 在
在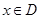 上恒成立
上恒成立 ;思路2:
;思路2:  在
在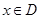 上恒成立
上恒成立 。
。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

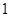





 ,
, ,
, .
.  ,
, ; (2) 若
; (2) 若 ,求
,求 的取值范围.
的取值范围. 的三个内角
的三个内角 依次成等差数列.
依次成等差数列. ,试判断
,试判断 ,求
,求
 中,
中, ,
, ,
, 分别为内角
分别为内角 ,
, ,
, 所对的边,且满足
所对的边,且满足 .
. ,且
,且 ,
, ,求
,求 的值.
的值. 展开式中,求:
展开式中,求: 平面ABCD,AD//BC//FE,AB
平面ABCD,AD//BC//FE,AB AD.
AD. ?若存在,试确定点M的位置;若不存在,请说明理由.
?若存在,试确定点M的位置;若不存在,请说明理由.