某四棱锥的三视图如图所示.该四棱锥的表面积是( )A．16$\sqrt{2}$B．16+16$\sqrt{2}$C．32$\sqrt{2}$D．16+32$\sqrt{2}$ 题目和参考答案——青夏教育精英家教网——

题目内容

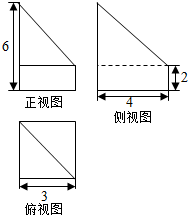
1．某四棱锥的三视图如图所示，该四棱锥的表面积是（　　）

A．

16$\sqrt{2}$

B．

16+16$\sqrt{2}$

C．

32$\sqrt{2}$

D．

16+32$\sqrt{2}$

分析由已知中的三视力可得该几何体是一个四棱锥，求出各个面的面积，相加可得答案．

解答解：由已知中的三视力可得该几何体是一个四棱锥，
棱锥的底面边长为4，故底面面积为16，
棱锥的高为2，故侧面的高为：2$\sqrt{2}$，
则每个侧面的面积为：$\frac{1}{2}×4×2\sqrt{2}$=4$\sqrt{2}$，
故棱锥的表面积为：16+16$\sqrt{2}$，
故选：B

点评本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．

练习册系列答案

领航中考系列答案

领跑中考系列答案

龙门之星系列答案

初中毕业学业考试指南系列答案

绿色新课堂中考总复习系列答案

中考数学合成演练30天系列答案

汇测期末竞优系列答案

素质提优123系列答案

随堂练123系列答案

随堂新卷系列答案

相关题目

11．已知点P（x₀，y₀）在直线L：4x+5y+20=0的左下方，则4x₀+5y₀+20的值（　　）

符号不能确定

12．已知数列{a_n}满足：a₁=$\frac{1}{2}$，a_n+1=$\frac{1}{{2-{a_n}}}$
（Ⅰ）求a₂，a₃；
（Ⅱ）求数列{a_n}的通项公式；
（Ⅲ）数列{a_n}的前n项和S_n；证明s_n＜n-ln$\frac{n+2}{2}$．

9．在数列{a_n}中，已知a₁=1，a_n+2=$\frac{1}{{{a_n}+1}}$，a₁₀₀=a₉₆，则a₁₁+a₁₂=$\frac{3}{26}±\frac{{\sqrt{5}}}{2}$．

16．某个几何体的三视图如图所示，则该几何体的体积是（　　）

6．若函数f（x）对任意实数x，y都有f（x+y）=f（x）+f（y）成立，则f（0）=（　　）

13．如果两圆的方程是x²+y²=4和x²+y²-6x-8y+9=0，那么这两个圆的位置关系是（　　）

10．已知|$\overrightarrow{b}$|=3，$\overrightarrow{a}$在$\overrightarrow{b}$上的射影为$\frac{8}{3}$，则$\overrightarrow{a}$•$\overrightarrow{b}$=8．

11．sin95°sin35°+cos95°cos35°=（　　）

$\frac{{\sqrt{3}}}{2}$

-$\frac{{\sqrt{3}}}{2}$