题目内容
 如图,已知⊙C过焦点A(0,P)(P>0)圆心C在抛物线x2=2py上运动,若MN为⊙C在x轴上截得的弦,设|AM|=l1,|AN|=l2,∠MAN=θ
如图,已知⊙C过焦点A(0,P)(P>0)圆心C在抛物线x2=2py上运动,若MN为⊙C在x轴上截得的弦,设|AM|=l1,|AN|=l2,∠MAN=θ(1)当C运动时,|MN|是否变化?证明你的结论.
(2)求
| l2 |
| l1 |
| l1 |
| l2 |
分析:(1)先设出圆的方程,求出M,N两点的坐标表示出|MN|即可发现|MN|的取值是否变化.
(2)由(1)可设M(x-p,0)、M(x+p,0),先利用两点间的距离公式求出 l1,l2,,代入
+
整理为关于p的函数,结合基本不等式求出其最大值和此时圆C的方程即可.
(2)由(1)可设M(x-p,0)、M(x+p,0),先利用两点间的距离公式求出 l1,l2,,代入
| l1 |
| l2 |
| l2 |
| l1 |
解答:解:(1)设C(x1,y1),⊙C方程为(x-x1)2+(y-y1)2=|AC|2
∴(x-x1)2+(y-y1)2=x12+(y1-P)2与y=0联立
得x2-2x1x+2y1p-p2=0…(2分)
∴|MN|=
=
∵C(x1,y1)在抛物线上
∴x12=2py1,代入|MN|
得|MN|=
=2p为定值
∴|MN|不变
(2)由(1)可设M(x-p,0)、M(x+p,0),
=
,
=
∴
+
=
=
=
=
=2•
=2
=2
≤2
当且仅当y=p时取等号,即x=±
p
∴圆方程为(x±
p)2+(y-p)2=2p2
当x=
p时,∠MAN为AM到AN的角KAM=
KAN=
∴tan∠MAN=
=1
∴∠θ=45°
同理,x=-
p时,∠MAN为AN到AM的角仍可得∠θ=45°
∴(x-x1)2+(y-y1)2=x12+(y1-P)2与y=0联立
得x2-2x1x+2y1p-p2=0…(2分)
∴|MN|=
|
4
|
∵C(x1,y1)在抛物线上
∴x12=2py1,代入|MN|
得|MN|=
| 4p2 |
∴|MN|不变
(2)由(1)可设M(x-p,0)、M(x+p,0),
| l | 1 |
(x-p
|
| l | 2 |
(x+p
|
∴
| ||
|
| ||
|
| ||||
|
2
| ||||||||||||
|
2
| ||||||
|
=
4py+4
| ||||||||
|
| y+p | ||||||
|
1+
|
1+
|
| 2 |
当且仅当y=p时取等号,即x=±
| 2 |
∴圆方程为(x±
| 2 |
当x=
| 2 |
| p |
| p-x |
| p |
| -(x-p) |
∴tan∠MAN=
| KAN-KAM |
| 1+KAN•KAM |
∴∠θ=45°
同理,x=-
| 2 |
点评:本题是对圆与抛物线以及基本不等式,距离公式等知识的综合考查,考查运算求解能力,考查化归与转化思想.属于中档题.

练习册系列答案
相关题目
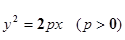 的焦点F恰好是双曲线
的焦点F恰好是双曲线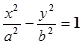 的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )
的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )
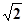 B.
B.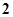 C.
C.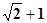 D.
D.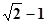
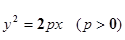 的焦点F恰好是双曲线
的焦点F恰好是双曲线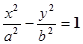 的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )
的右焦点,且两条曲线的交点的连线过F,则该双曲线的离心率为( )
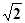 B.
B.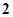 C.
C.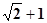 D.
D.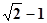
 的最大值,并求出取最大值时θ值及此时⊙C方程.
的最大值,并求出取最大值时θ值及此时⊙C方程.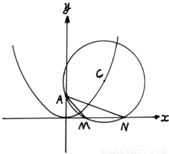
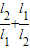 的最大值,并求出取最大值时θ值及此时⊙C方程.
的最大值,并求出取最大值时θ值及此时⊙C方程.