题目内容
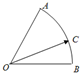
如图,在扇形OAB中,∠AOB=60°,C为弧AB上且与A,B不重合的一个动点,
=x
+y
,若u=x+λy,(λ>0)存在最大值,则λ的取值范围为( )
| OC |
| OA |
| OB |
A.(
| B.(1,3) | C.(
| D.(
|


设射线OB上存在为B',使
| OB′ |
| 1 |
| λ |
| OB |
由于
| OC |
| OA |
| OB |
| OA |
| 1 |
| λ |
| OB |
| OA |
| OB′ |
设
| OC |
| OC′ |
| OC′ |
| OA |
| OB′ |
由A,B',C'三点共线可知x'+λy'=1,
所以u=x+2y=tx'+t•2y'=t,
则u=
|
| ||
|
|
即在弧AB(不包括端点)上存在与AB'平行的切线,
所以λ∈(
| 1 |
| 2 |
故选C.

练习册系列答案
相关题目
 如图,在扇形OAB中,∠AOB=90°,C为
如图,在扇形OAB中,∠AOB=90°,C为
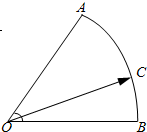 (2013•杭州一模)如图,在扇形OAB中,∠AOB=60°,点C为弧AB上的一个动点.若
(2013•杭州一模)如图,在扇形OAB中,∠AOB=60°,点C为弧AB上的一个动点.若 如图,在扇形OAB中,∠AOB=60°,C为弧AB上且与A,B不重合的一个动点,
如图,在扇形OAB中,∠AOB=60°,C为弧AB上且与A,B不重合的一个动点, ,若u=x+λy,(λ>0)存在最大值,则λ的取值范围为( )
,若u=x+λy,(λ>0)存在最大值,则λ的取值范围为( )


