题目内容
 如图,在扇形OAB中,∠AOB=90°,C为
如图,在扇形OAB中,∠AOB=90°,C为 |
| AB |
 |
| AB |
分析:由于点N随机地落在线段OC上,故可以认为点N落在线段OC上任一点是等可能的,可将线段OC看做区域D,以线段长度为“测度”来计算.
解答: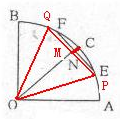 解:如图,当且仅当PQ=OA时,即N点在线段OC上的点M处时,
解:如图,当且仅当PQ=OA时,即N点在线段OC上的点M处时,
△POQ为正三角形,∠MOP=30°,
设半圆的半径为R,
则OM=
OP=
R
又因为N对线段OC上的所有的点都是等可能的,
所以在线段OC上任取一点N,使得ON>OC?EF<OA,
则EF<OA的概率为:
=
=1-
.
故答案为:1-
.
 解:如图,当且仅当PQ=OA时,即N点在线段OC上的点M处时,
解:如图,当且仅当PQ=OA时,即N点在线段OC上的点M处时,△POQ为正三角形,∠MOP=30°,
设半圆的半径为R,
则OM=
| ||
| 2 |
| ||
| 2 |
又因为N对线段OC上的所有的点都是等可能的,
所以在线段OC上任取一点N,使得ON>OC?EF<OA,
则EF<OA的概率为:
| MC |
| OC |
R-
| ||||
| R |
| ||
| 2 |
故答案为:1-
| ||
| 2 |
点评:本题主要考查了几何概型,如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称为几何概型.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
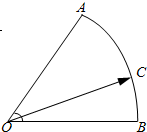 (2013•杭州一模)如图,在扇形OAB中,∠AOB=60°,点C为弧AB上的一个动点.若
(2013•杭州一模)如图,在扇形OAB中,∠AOB=60°,点C为弧AB上的一个动点.若 如图,在扇形OAB中,∠AOB=60°,C为弧AB上且与A,B不重合的一个动点,
如图,在扇形OAB中,∠AOB=60°,C为弧AB上且与A,B不重合的一个动点,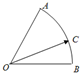
 ,若u=x+λy,(λ>0)存在最大值,则λ的取值范围为( )
,若u=x+λy,(λ>0)存在最大值,则λ的取值范围为( )


