题目内容
12．
从某企业生产的某种产品中抽取100件，测量这些产品的质量指标值，由测量结果得到如图所示的频率分布直方图，质量指标值落在区间[55，65），[65，75），[75，85]内的频率之比为4：2：1．若将频率视为概率，从该企业生产的这种产品中随机抽取3件，记这3件产品中质量指标值位于区间[45，75）内的产品件数为X，则X数学期望为1.8．
分析 求出产品指标落在各区间的产品个数，得出一件产品的质量指标落在区间[45，75）内的概率，利用二项分布的数学期望公式计算．
解答 解：质量指标落在[55，85]的产品件数为100×[1-（0.004+0.012+0.019+0.030）×10]=35，
∴质量指标落在[55，65），[65，75），[75，85]内的产品件数分别为20，10，5，
又质量指标落在[45，55]的产品件数为100×0.030×10=30，
∴质量指标值位于区间[45，75）内的产品件数为30+20+10=60，
∴从该企业生产的这种产品中随机抽取1件，这件产品质量指标值位于区间[45，75）内的概率为$\frac{60}{100}$=0.6．
∴X～B（3，0.6），
∴X的数学期望为3×0.6=1.8．
故答案为：1.8．
点评 本题考查了频率分布直方图，二项分布，属于中档题．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
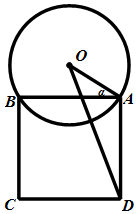某校一个校园景观的主题为“托起明天的太阳”，其主体是一个半径为5米的球体，需设计一个透明的支撑物将其托起，该支撑物为等边圆柱形的侧面，厚度忽略不计．轴截面如图所示，设∠OAB=α．（注：底面直径和高相等的圆柱叫做等边圆柱．）
在正方体ABCD-A1B1C1D1中，M、N、P分别是AD1、BD和B1C的中点．
1．已知△ABC中，b=2，B=45°，C=105°，则a=（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$+1 | C． | $\sqrt{3}$-1 | D． | $\sqrt{3}$ |