题目内容
11.已知函数$f(x)=\left\{{\begin{array}{l}{|{lgx}|(0<x≤10)}\\{-\frac{1}{2}x+6(x>10)}\end{array}}\right.$若a<b<c,且f(a)=f(b)=f(c),则$3ab+\frac{c}{{{a^2}{b^2}}}$的取值范围是( )| A. | (4,13) | B. | (8,9) | C. | (23,27) | D. | (13,15) |
分析 画出图象得出当f(a)=f(b)=f(c),a<b<c时,0<a<1<b<c<12,ab=1,化简3ab+$\frac{c}{{{a}^{2}b}^{2}}$=3+c,即可求解范围
解答 解:函数$f(x)=\left\{{\begin{array}{l}{|{lgx}|(0<x≤10)}\\{-\frac{1}{2}x+6(x>10)}\end{array}}\right.$,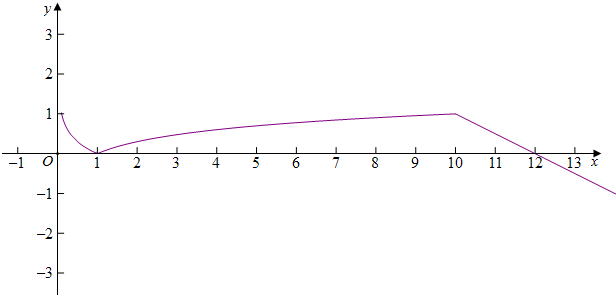
f(a)=f(b)=f(c),a<b<c,
∴0<a<1<b<c<12,ab=1,
∴3ab+$\frac{c}{{{a}^{2}b}^{2}}$=3+c,
13<3+c<15,
故选:D.
点评 本题考查了函数的性质,运用图象得出a,b,c的范围,关键是得出ab=1,代数式的化简,不等式的运用,属于中档题

练习册系列答案
相关题目
19.设全集I=R,若集合M={y|y=2${\;}^{\sqrt{3+2x-{x}^{2}}}$},N={x|y=ln(x-2)},则M∩∁I(N)=( )
| A. | [2,4] | B. | [1,2] | C. | (-∞,2]∪[4,+∞) | D. | (-∞,1]∪[2,+∞) |
6.f(x)为奇函数,且在(-∞,0)为递增,f(-2)=0,则xf(x)>0的解集为( )
| A. | (-∞,-2)∪(2,+∞) | B. | (-∞,-2)∪(0,2) | C. | (-2,0)∪(0,2) | D. | (-2,0)∪(2,+∞) |
16.已知向量$\overrightarrow{a}$(3,1),$\overrightarrow{b}$=(x,-4),若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则实数x的值为( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | -$\frac{3}{4}$ | D. | -$\frac{4}{3}$ |
3.有下列四个命题:
(1)“若xy>0,则x,y同正、或同负”的逆命题
(2)“周长相等的两个三角形全等”的否命题
(3)“若m≤1,则x2-2x+m=0有实数解”的逆否命题
(4)“若A∩B=B,则A⊆B”的逆否命题
其中真命题为( )
(1)“若xy>0,则x,y同正、或同负”的逆命题
(2)“周长相等的两个三角形全等”的否命题
(3)“若m≤1,则x2-2x+m=0有实数解”的逆否命题
(4)“若A∩B=B,则A⊆B”的逆否命题
其中真命题为( )
| A. | (1)(2) | B. | (2)(3) | C. | (3)(4) | D. | (1)(2)(3) |