题目内容

7．正项数列{an}满足an2+3an=6Sn+10，则an=3n+2．

分析 利用等差数列的通项公式、递推关系即可得出．

解答 解：∵正项数列{an}满足an2+3an=6Sn+10，
∴当n=1时，${a}_{1}^{2}+3{a}_{1}$=6a1+10，解得a1=5．
当n≥2时，${a}_{n-1}^{2}+3{a}_{n-1}$=6Sn-1+10，
可得${a}_{n}^{2}-{a}_{n-1}^{2}$+3（an-an-1）=6an，
化为：（an+an-1）（an-an-1-3）=0，
∴an-an-1=3，
∴数列{an}是等差数列，首项为5，公差为3．
∴an=5+3（n-1）=3n+2．
故答案为：3n+2．

点评 本题考查了等差数列的通项公式、递推关系，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
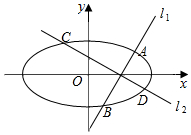17．在平面直角坐标系中，已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{3}}{2}$，F为椭圆的右焦点，过点F任作一条直线l1，交椭圆E于A，B两点，当l1垂直于x轴时，|AB|=1．
（1）求椭圆E的标准方程；
（2）过F再作一条直线l2，使得l1⊥l2，且l2交椭圆于C，D两点，试问$\frac{1}{|AF|}$+$\frac{1}{|BF|}$+$\frac{1}{|CF|}$+$\frac{1}{|DF|}$是否为定值，说明理由．
18．已知$\frac{z-1}{z+1}$是纯虚数，则|z2-z+1|的最大值是[0，3）．
15．若数列{an}中，a1=$\frac{1}{3}$，an+1=$\frac{n+1}{3n}$an．
（1）证明：数列{$\frac{{a}_{n}}{n}$}的是等比数列，
（2）求{an}的通项公式；
（3）求数列{an}前n项和为Sn．
2．（x+$\frac{1}{x}$+1）6的展开式中常数项为141．
12．已知a1=1，an+1-an=3n+2．则通项an=$\frac{3{n}^{2}-2n+1}{2}$．
19．若$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$是夹角为60°的两个单位向量，求证：（2$\overrightarrow{{e}_{2}}$$-\overrightarrow{{e}_{1}}$）⊥$\overrightarrow{{e}_{1}}$．
16．圆x2+y2=1上的点到3x+4y+25=0的最短距离是（　　）
A．1B．5C．4D．6
15．函数$g（θ）={sin^2}θ+mcosθ-2m，θ∈[{0，\frac{π}{2}}]$．
（1）当m=$\sqrt{3}$时，求g（θ）的单调递增区间；
（2）若g（θ）+1＜0恒成立，求m的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网