题目内容
2.(x+$\frac{1}{x}$+1)6的展开式中常数项为141.分析 根据(x+$\frac{1}{x}$+1)6的展开式的通项公式,得出产生常数项的情况是x与$\frac{1}{x}$的次数相同时,由此求出展开式的常数项.
解答 解:(x+$\frac{1}{x}$+1)6的展开式的通项公式为Tr+1=${C}_{6}^{r}$•${(x+\frac{1}{x})}^{r}$•16-r=${C}_{6}^{r}$•${(x+\frac{1}{x})}^{r}$;
令r=0,求得常数为${C}_{6}^{0}$=1,
令r=2,求得常数为${C}_{6}^{2}$•2=30,
令r=4,求得常数为${C}_{6}^{4}$•${C}_{4}^{2}$=90,
令r=6,求得常数为${C}_{6}^{6}$•${C}_{6}^{3}$=20;
所以展开式中常数项为1+30+90+20=141.
故答案为:141.
点评 本题考查了二项式展开式通项公式的应用问题,解题的关键是得出产生常数项的情况为哪些,是基础题目.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
11.$\underset{lim}{n→∞}$$\frac{{1}^{p}{+2}^{p}{+3}^{p}+…{+n}^{p}}{{n}^{p+1}}$(p>0)可表示成定积分( )
| A. | ${∫}_{0}^{1}$$\frac{1}{x}$dx | B. | ${∫}_{0}^{1}$xpdx | C. | ${∫}_{0}^{1}$($\frac{1}{x}$)pdx | D. | ${∫}_{0}^{1}$($\frac{x}{n}$)pdx |
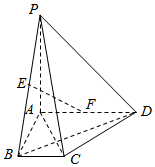 如图,在四棱锥P-ABCD中,PA⊥面ABCD,AD∥BC,∠BAD=90°,BC=1,AD=PA=$\sqrt{2}$AB=2,E,F分别为PB,AD的中点.
如图,在四棱锥P-ABCD中,PA⊥面ABCD,AD∥BC,∠BAD=90°,BC=1,AD=PA=$\sqrt{2}$AB=2,E,F分别为PB,AD的中点.