题目内容
13.把复数z的共轭复数记作$\overline{z}$,i为虚数单位,若z=1+i.(1)求复数(1+z)•$\overline{z}$;
(2)求(1+$\overline{z}$)•z2的模.
分析 (1)求出$\overline{z}$=1-i,再根据复数的代数形式的运算即可求出,
(2)根据复数的代数形式的运算化简,再根据复数模的计算即可.
解答 解:(1)∵z=1+i,
∴$\overline{z}$=1-i,
∴(1+z)•$\overline{z}$=(2+i)(1-i)=2-2i+i-i2=3-i,
(2)(1+$\overline{z}$)•z2=(2-i)(1+i)2=(2-i)•2i=2+4i,
∴|(1+$\overline{z}$)•z2|=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$.
点评 本题考查复数的代数形式的运算,涉及共轭复数复数的模,属基础题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
8.已知A(1,2),B(5,4),C(x,3),D(-3,y),且$\overrightarrow{AB}$=$\overrightarrow{CD}$,则x,y的值分别为( )
| A. | -7,-5 | B. | 7,-5 | C. | -7,5 | D. | 7,5 |
18.已知tanα=3,则cos2α=( )
| A. | $\frac{9}{10}$ | B. | -$\frac{9}{10}$ | C. | -$\frac{4}{5}$ | D. | $\frac{4}{5}$ |
5.二次函数f(x)的图象如图所示,则f(x-1)>0的解集为( )
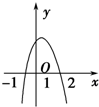

| A. | (-2,1) | B. | (0,3) | C. | (-1,2] | D. | (-∞,0)∪(3,+∞) |
3.袋中有2个红色的变形金刚,2个白色的变形金刚,2个黑色的变形金刚,从里面任意取2个变形金刚,不是基本事件的为( )
| A. | {恰好2个红色的变形金刚} | B. | {恰好2个黑色的变形金刚} | ||
| C. | {恰好2个白色的变形金刚} | D. | {至少1个红色的变形金刚} |