��Ŀ����
����Ŀ���ٶ�С���������x���������Ч��y֮�������ع�ϵ������5���������£�
x | 15.0 | 25.58 | 30.0 | 36.6 | 44.4 |
y | 39.4 | 42.9 | 42.9 | 43.1 | 49.2 |
(1)��xΪ���ͱ�����yΪԤ������������ɢ��ͼ��
(2)��y��x֮������Իع鷽�̣����ڻ�������56.7Ԥ������Ч�룻
(3)�������в������в�ƽ���ͣ�
(4)��R2����˵���в��������Ч���Ӱ��ռ�ٷ�֮����
���𰸡�(1)������ ��2��![]() ��0.29x��34.708�����Ƴ�������Ч��51.151. (3)
��0.29x��34.708�����Ƴ�������Ч��51.151. (3) ![]() ��0.342��
��0.342�� ![]() ��0.773 8��
��0.773 8�� ![]() ����0.508��
����0.508�� ![]() ����2.222��
����2.222�� ![]() ��1.616.
��1.616. ![]() ��8.521 30.(4) R2��0.830���в����������Լ1��83%��17%.
��8.521 30.(4) R2��0.830���в����������Լ1��83%��17%.
�����������������(1)��������ϵ���ݸ���ֵ���ÿ���㼴�ɣ�2����ͼ���������������״�ֲ����бȽϺõ�������ع�ϵ����˿��������Իع鷽�̻̿�����֮��Ĺ�ϵ�����ݱ������ݣ�����![]() ��
�� ![]() ��
��![]() д�����Իع鷽�̣�����x��56.7ʱ���ý⣨3������y��bx��a��e���������
д�����Իع鷽�̣�����x��56.7ʱ���ý⣨3������y��bx��a��e���������![]() ��yi��
��yi��![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ��0.342��
��0.342�� ![]() ��0.773 8��
��0.773 8�� ![]() ����0.508��
����0.508�� ![]() ����2.222��
����2.222�� ![]() ��1.616.������ͼ����ܲв�ƽ���ͣ�4��������ƫ��ƽ���ͣ��ع�ƽ����=��ƫ��ƽ����-�в�ƽ���ͣ����빫ʽ��R2�����ͱ���С�������������ЧӦ�����ã��в����������.
��1.616.������ͼ����ܲв�ƽ���ͣ�4��������ƫ��ƽ���ͣ��ع�ƽ����=��ƫ��ƽ����-�в�ƽ���ͣ����빫ʽ��R2�����ͱ���С�������������ЧӦ�����ã��в����������.
���������
(1)����ͼ��ʾ��
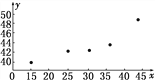
(2)��ͼ���������������״�ֲ����бȽϺõ�������ع�ϵ����˿��������Իع鷽�̻̿�����֮��Ĺ�ϵ����ع鷽��Ϊ![]() ��
��![]() x��
x��![]() ��
��![]() ��30.316��
��30.316��![]() ��43.5��
��43.5��![]() ��5 090.256 4��
��5 090.256 4��
![]() ��
��![]() ��1 318.746��
��1 318.746��![]() 2��1 892.25��
2��1 892.25��![]() 2��919.059 9��
2��919.059 9��
![]() iyi��6 737.322.
iyi��6 737.322.
��![]() ��
��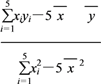 ��0.29.
��0.29.![]() ��
��![]() ��
��![]()
![]() ��34.708.
��34.708.
����������Իع鷽��Ϊ![]() ��0.29x��34.708.
��0.29x��34.708.
��x��56.7ʱ��![]() ��0.29��56.7��34.708��51.151�����Ƴ�������Ч��51.151.
��0.29��56.7��34.708��51.151�����Ƴ�������Ч��51.151.
(3)����y��bx��a��e���������![]() i��yi��
i��yi��![]() i�ֱ�Ϊ
i�ֱ�Ϊ![]() ��0.342��
��0.342�� ![]() ��0.773 8��
��0.773 8�� ![]() ����0.508��
����0.508�� ![]() ����2.222��
����2.222�� ![]() ��1.616.
��1.616.
�в�ƽ���ͣ�![]() ��8.521 30.
��8.521 30.
(4)��ƫ��ƽ���ͣ�![]() (yi��
(yi��![]() )2��50.18��
)2��50.18��
�ع�ƽ���ͣ�50.18��8.521 30��41.658 7��
R2��0.830.
����ͱ���С�������������ЧӦ������Լ83%.
�в����������Լ1��83%��17%.

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�