题目内容
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() ),直线
),直线![]() 的极坐标方程为
的极坐标方程为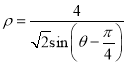 .
.
(1)写出曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)![]() 为曲线
为曲线![]() 上任意一点,
上任意一点, ![]() 为直线
为直线![]() 任意一点,求
任意一点,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;
; ![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)曲线![]() 消去
消去![]() 可得普通方程,注意参数的范围,利用极直互化可得直线的直角坐标方程;
可得普通方程,注意参数的范围,利用极直互化可得直线的直角坐标方程;
(2)圆上的点到直线的距离可以转化为圆心到直线的距离求解.
试题解析:
(1)曲线![]() 的参数方程为
的参数方程为![]() ,(
,( ![]() 为参数,
为参数, ![]() ),
),
消去参数![]() ,可得
,可得![]() ,
,
由于![]() ,∴
,∴![]() ,
,
故曲线![]() 的轨迹方程是上半圆
的轨迹方程是上半圆![]() .
.
∵直线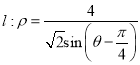 ,即
,即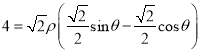 ,即
,即![]() ,
,
故直线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(2)由题意可得点![]() 在直线
在直线![]() 上,点
上,点![]() 在半圆上,半圆的圆心
在半圆上,半圆的圆心![]() 到直线
到直线![]() 的距离等于
的距离等于![]() ,即
,即![]() 的最小值为
的最小值为![]() .
.

【题目】某年级举办团知识竞赛.![]() 、
、![]() 、
、![]() 、
、![]() 四个班报名人数如下:
四个班报名人数如下:
班别 |
|
|
|
|
人数 | 45 | 60 | 30 | 15 |
年级在报名的同学中按分层抽样的方式抽取10名同学参加竞赛,每位参加竞赛的同学从10个关于团知识的题目中随机抽取4个作答,全部答对的同学获得一份奖品.
(Ⅰ)求各班参加竞赛的人数;
(Ⅱ)若![]() 班每位参加竞赛的同学对每个题目答对的概率均为
班每位参加竞赛的同学对每个题目答对的概率均为![]() ,求
,求![]() 班恰好有2位同学获得奖品的概率;
班恰好有2位同学获得奖品的概率;
(Ⅲ)若这10个题目,小张同学只有2个答不对,记小张答对的题目数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
【题目】为了丰富退休生活,老王坚持每天健步走,并用计步器记录每天健步走的步数.他从某月中随机抽取20天的健步走步数(老王每天健步走的步数都在![]() 之间,单位:千步),绘制出频率分布直方图(不完整)如图所示.
之间,单位:千步),绘制出频率分布直方图(不完整)如图所示.
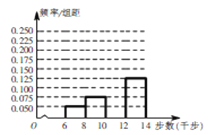
(1)完成频率分布直方图,并估计该月老王每天健步走的平均步数(每组数据可用区间中点值代替;
(2)某健康组织对健步走步数的评价标准如下表:
每天步数分组(千步) |
|
|
|
评价级别 | 及格 | 良好 | 优秀 |
现从这20天中评价级别是“及格”或“良好”的天数里随机抽取2天,求这2天的健步走结果属于同一评价级别的概率.
【题目】假定小麦基本苗数x与成熟期有效穗y之间存在相关关系,今测得5组数据如下:
x | 15.0 | 25.58 | 30.0 | 36.6 | 44.4 |
y | 39.4 | 42.9 | 42.9 | 43.1 | 49.2 |
(1)以x为解释变量,y为预报变量,作出散点图;
(2)求y与x之间的线性回归方程,对于基本苗数56.7预报其有效穗;
(3)计算各组残差,并计算残差平方和;
(4)求R2,并说明残差变量对有效穗的影响占百分之几.
