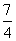题目内容
已知两点A(2,3),B(4,1),直线l:x+2y-2=0,在直线l上求一点P.
(1)使|PA|+|PB|最小;
(2)使|PA|-|PB|最大.
解析:(1)可判断A,B在直线l的同侧,设A点关于l的对称点A1的坐标为(x1,y1).
则有 解得
解得 由两点式求得直线A1B的方程为y=
由两点式求得直线A1B的方程为y= +1,直线A1B与l的交点可求得P
+1,直线A1B与l的交点可求得P .由平面几何知识可知|PA|+|PB|最小.
.由平面几何知识可知|PA|+|PB|最小.
(2)由两点式求得直线A B的方程为y-1=-(x-4),即x+y-5=0.
B的方程为y-1=-(x-4),即x+y-5=0.
直线AB与l的交点可求得P(8 ,-3),它使|PA|-|PB|最大.
,-3),它使|PA|-|PB|最大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 +
+ 的最小值为( )
的最小值为( ) C.5 D.7
C.5 D.7 .-1或3
.-1或3 x+b的图象关于直线y=x对称,则a+b=____________.
x+b的图象关于直线y=x对称,则a+b=____________.

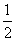 x2上横坐标大于零的一点,直线l过点P并与抛物线C在点P处的切线垂直,直线l与抛物线C相交于另一点Q.
x2上横坐标大于零的一点,直线l过点P并与抛物线C在点P处的切线垂直,直线l与抛物线C相交于另一点Q.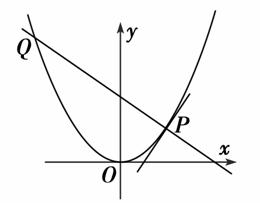
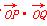 =0,求过点P,Q,O的圆的方程.
=0,求过点P,Q,O的圆的方程.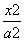
 -
-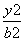 =1的焦距为10,点P(2,1)在C 的渐近线上,则C的方程为( )
=1的焦距为10,点P(2,1)在C 的渐近线上,则C的方程为( ) -
- =1 B.
=1 B. -
- =1
=1 -
- -
- =1
=1 y2=x的焦点,A,B是该抛物线上的两点,|AF|+|BF|=3,则线段AB的中点到y轴的距离为( )
y2=x的焦点,A,B是该抛物线上的两点,|AF|+|BF|=3,则线段AB的中点到y轴的距离为( )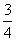 B.1 C.
B.1 C.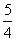 D.
D.