题目内容
已知向量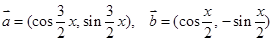
，
设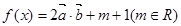
，
（1）求函数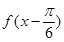
在
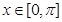上的单调递增区间；
（2）当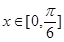
时，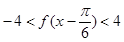
恒成立，求实数
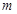的取值范围.
【答案】
（1）函数
（2）
【解析】(1)先确定
,
然后可得
,再借助余弦函数的增区间来求其增区间即可.
(2) 函数在
上的单调递增，可得的最大值m+3,最小值为m+2.
所以
恒成立转化为
,解此不等式组即可求出m的取值范围解：（1）
∴
由
可得函数的单调递增区间为
又∵
∴函数
……………………6分
（2）∵函数在上的单调递增，
∴的最大值为
，最小值为
∵恒成立
∴
∴
……………………14分
练习册系列答案
相关题目
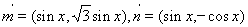
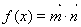
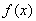
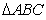
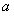
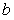
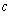
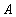
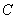
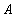
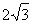
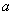
，设函数
；
求函数f（x）的最值及对应的x的值；-
恒成立，求实数m的取值范围．
，设函数
且f（x）的最小正周期为2π．
，求证：f（x）＞g（x）．
，设函数
.
在
上的单调递增区间；
中，
，
，
分别是角
，
，
的对边，
，
，
，求边
，设向量
，则
。