题目内容
用反证法证明命题:“如果a>b>0,那么|a|>|b|”时,假设的内容应是( )
| A、|a|=|b| |
| B、|a|<|b| |
| C、|a|≤|b| |
| D、|a|>|b|且|a|=|b| |
考点:反证法与放缩法
专题:证明题,反证法,推理和证明
分析:结论|a|>|b|的否定为:|a|≤|b|,由此得出结论.
解答:
解:由于结论|a|>|b|的否定为:|a|≤|b|,
用反证法证明命题时,要首先假设结论的否定成立,
故应假设:|a|≤|b|,由此推出矛盾.
故选:C.
用反证法证明命题时,要首先假设结论的否定成立,
故应假设:|a|≤|b|,由此推出矛盾.
故选:C.
点评:本题主要考查用反证法证明数学命题,把要证的结论进行否定,得到要证的结论的反面,从而得到所求,属于基础题.

练习册系列答案
相关题目
已知函数y=f(x)的图象如图,则满足f(
)•f(5)≤0的x取值范围为( )
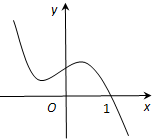
| 2x+1 |
| x-1 |

| A、[-2,1) |
| B、[-1,1] |
| C、[1,2] |
| D、[2,3] |
已知如图程序框图,则输出的i是( )


| A、9 | B、11 | C、13 | D、15 |