题目内容
6.已知A={α|sinα≤$\frac{\sqrt{2}}{2}$,α∈[0,2π)},B={β|cosβ≤$\frac{\sqrt{2}}{2}$,β∈[0,2π)},则A∩B=$\{\frac{π}{4}\}$∪$[\frac{3π}{4},\frac{7π}{4}]$.分析 利用三角函数的单调性可得:A=$[0,\frac{π}{4}]$∪$[\frac{3π}{4},2π)$,B=$[\frac{π}{4},\frac{7π}{4}]$,再利用交集运算性质即可得出.
解答 解:A={α|sinα≤$\frac{\sqrt{2}}{2}$,α∈[0,2π)}=$[0,\frac{π}{4}]$∪$[\frac{3π}{4},2π)$,
B={β|cosβ≤$\frac{\sqrt{2}}{2}$,β∈[0,2π)}=$[\frac{π}{4},\frac{7π}{4}]$,
则A∩B=($[0,\frac{π}{4}]$∪$[\frac{3π}{4},2π)$)∩$[\frac{π}{4},\frac{7π}{4}]$=$\{\frac{π}{4}\}$∪$[\frac{3π}{4},\frac{7π}{4}]$,
故答案为:$\{\frac{π}{4}\}$∪$[\frac{3π}{4},\frac{7π}{4}]$.
点评 本题考查了三角函数的单调性、交集运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
16.P为边长为2的正三角形内(不包括边界)一点,P到三角形三边距离分别为a、b、c,则ab+bc+ca取值范围是( )
| A. | (0,1] | B. | (0,2) | C. | $({0,2\sqrt{3}})$ | D. | (0,4) |
14.下列各组函数中是同一函数的是( )
| A. | $y=\frac{x^2}{x}$与y=x | B. | $y=\sqrt{x^2}$与y=x | C. | y=x0与y=1 | D. | $y=\root{3}{x^3}$与y=x |
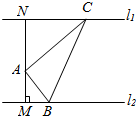 如图,A是两条平行直线之间的一定点,且点A到两平行直线的距离分别为AM=1,AN=$\sqrt{2}$,设△ABC,AC⊥AB,且顶点B、C分别在两平行直线上运动,则
如图,A是两条平行直线之间的一定点,且点A到两平行直线的距离分别为AM=1,AN=$\sqrt{2}$,设△ABC,AC⊥AB,且顶点B、C分别在两平行直线上运动,则