题目内容
12.已知等比数列{an}中,a3=16,且a1a2…a10=265,求{an}的通项公式.分析 设出等比数列的首项和公比,由题意列方程组求得首项和公比,则{an}的通项公式可求.
解答 解:设等比数列{an}的首项为a1,公比为q,由已知,得
$\left\{\begin{array}{l}{{a}_{1}{q}^{2}=16}\\{{{a}_{1}}^{10}{q}^{45}={2}^{65}}\end{array}\right.$,解得$\left\{\begin{array}{l}{{a}_{1}=4}\\{q=2}\end{array}\right.$.
∴an=4×2n-1=2n+1,
即{an}的通项公式是an=2n+1.
点评 本题考查等比数列的通项公式,考查了计算能力,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.设f(x)是定义在(-∞,+∞)上的减函数,且x1+x2>0,则( )
| A. | f(x1)>f(-x2) | B. | f(-x1)>f(-x2) | C. | f(x1)<f(-x2) | D. | f(-x1)<f(-x2) |
1.已知圆C:x2+y2-4x=0,l的方程为mx-3m+y=0,则( )
| A. | l与C相交 | B. | l与C相切 | ||
| C. | l与C相离 | D. | 以上三个选项均有 |
2.设函数f(x)=$\left\{\begin{array}{l}{{x}^{2}-4x+1\\;x≥0}\\{3x+2\\;x<0}\end{array}\right.$若互不相等的实数x1,x2,x3满足f(x1)=f(x2)=f(x3),则x1+x2+x3的取值范围是( )
| A. | [$\frac{7}{3}$,+∞) | B. | [$\frac{7}{3}$,4) | C. | ($\frac{7}{3}$,$\frac{11}{3}$] | D. | ($\frac{11}{3}$,+∞) |
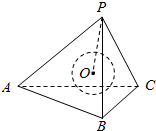 正三棱锥高为1,底面边长为2$\sqrt{6}$,内有一球与四个面都相切.
正三棱锥高为1,底面边长为2$\sqrt{6}$,内有一球与四个面都相切.