题目内容
已知1,2,…, 满足下列性质T的排列
满足下列性质T的排列 ,
, ,…,
,…, 的个数为
的个数为 (n≥2,且n∈N*).
(n≥2,且n∈N*).
性质T:排列 ,
, ,…,
,…, 中有且只有一个
中有且只有一个 (
( {1,2,…,
{1,2,…, }).
}).
(1)求 ;
;
(2)求 .
.
解:(1)当 时,1,2,3的所有排列有
时,1,2,3的所有排列有 ,2,
,2, ,
, ,3,
,3, ,
, ,1,
,1, ,
, ,3,
,3, ,
,
 ,1,
,1, ,
, ,2,
,2, ,其
,其 中满足仅存在一个
中满足仅存在一个 {1,2,3},使得
{1,2,3},使得 的排列有
的排列有
 ,3,
,3, ,
, ,1,
,1, ,
, ,3,
,3, ,
, ,1,
,1, ,
,
所以 .
.
(2)在1,2,…, 的所有排列
的所有排列 ,
, ,…,
,…, 中,
中,
若 ,从
,从 个数1,2,3,…,
个数1,2,3,…, 中选
中选 个数按从小到大的顺序
个数按从小到大的顺序
排列为 ,
, ,…,
,…, ,其余按从小到大的顺序排列在余下位置,于是满足题意的排列个数为
,其余按从小到大的顺序排列在余下位置,于是满足题意的排列个数为 .
.
若 ,则满足题意的排列个数为
,则满足题意的排列个数为 .
.
综上,


 .
.
| |

练习册系列答案
相关题目
 是偶函数,则
是偶函数,则 ( ).
( ).  B.
B. C.
C. D.
D.
 中,直线
中,直线 是曲线
是曲线 的切线,则当
的切线,则当 >0时,实数
>0时,实数 的最小值是 .
的最小值是 . 对任意实数
对任意实数 ,在闭区间
,在闭区间 上总存在两实数
上总存在两实数 、
、 ,使得
,使得 8成立,则实数
8成立,则实数 的最小值为 .
的最小值为 . 2AM.
2AM. AC.
AC. 的夹角为
的夹角为 ,且
,且 ,则
,则 与
与
 B.
B. D.
D.
 中,已知
中,已知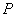 是函数
是函数 的图象上的动点,该图象
的图象上的动点,该图象 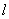 交
交 轴于点
轴于点 ,过点
,过点 .
.  的范围是
的范围是 B.
B.  C.
C.  D.
D. 

 ;
; ,试求
,试求 的大小.
的大小.