Question

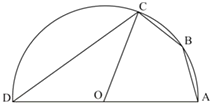（2010•温州二模）设AD是半径为5的半圆O的直径（如图），B，C是半圆上两点，AB=BC=

10

．
（1）求cos∠AOB的值；
（2）求

DC

•

DA

的值．

Answer 1

分析：（1）在△AOB中，利用余弦定理求解即可．
（2）根据圆的性质，得出∠CDA=

1

2

∠AOC=∠AOB．从而cos∠CDA=cos∠AOB=

4

5

，解直角三角形ACD，求出CD后，利向量的数量积公式计算．

解答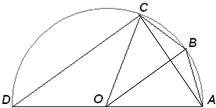：解：（1）连接OB，由余弦定理得
cos∠AOB=

OB2+OA2-AB2

2OA•OB

=

25+25-10

2•5•5

=

4

5

…（5分）
（2）连接AC，∵AD为直径，∴∠ACD=90°   …（7分）
又∵∠CDA=

1

2

∠AOC=∠AOB．
∴cos∠CDA=cos∠AOB=

4

5

  …（9分）
又cos∠CDA=

CD

DA

=

CD

10

，∴CD=8    …（12分）
∴

DC

•

DA

=|

DC|

•|

DA

|cos∠CDA=8×10×

4

5

=64   …（14分）

点评：本题考查余弦定理得应用，向量的数量积运算．用到了圆的性质，实现了角的等量代换．