题目内容
（2010•温州二模）设AD是半径为5的半圆O的直径（如图），B，C是半圆上两点，已知AB=BC=| 10 |
（1）求cos∠AOC的值．
（2）求
| DC |
| DB |
分析：（I）连接OB在△AOB中利用余弦定理求得cos∠AOB的值，利用AB=BC推断出∠AOC=2∠AOB，然后利用二倍角公式求得答案．
（II）根据题意可知ADC=∠AOB，∠ADB=∠BDC，进而求得|
|，在Rt△ADB中利用cos∠ADB求得|
|，则
•
的值可求．
（II）根据题意可知ADC=∠AOB，∠ADB=∠BDC，进而求得|
| DC |
| DB |
| DC |
| DB |
解答：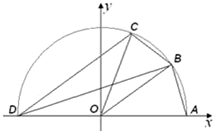
（I）解：如图，连接OB，由余弦定理得cos∠AOB=
=
，
由AB=BC知∠AOC=2∠AOB，
则cos∠AOC=2cos2∠AOB-1=
．
（Ⅱ）由题意可知：∠ADC=∠AOB，∠ADB=∠BDC，则|
|=8，
又在Rt△ADB中，可得cos∠ADB=
，|
|=3
，
故
•
=8×3
×
=72．
（I）解：如图，连接OB，由余弦定理得cos∠AOB=| 25+25-10 |
| 2×5×5 |
| 4 |
| 5 |
由AB=BC知∠AOC=2∠AOB，
则cos∠AOC=2cos2∠AOB-1=
| 7 |
| 25 |
（Ⅱ）由题意可知：∠ADC=∠AOB，∠ADB=∠BDC，则|
| DC |
又在Rt△ADB中，可得cos∠ADB=
| 3 | ||
|
| DB |
| 10 |
故
| DC |
| DB |
| 10 |
| 3 | ||
|
点评：本题主要考查了余弦定理的应用．考查了考生对解三角形问题基本方法和基本公式的熟练掌握．
练习册系列答案
阅读快车系列答案
相关题目