题目内容
17.在平面内,若有|$\overrightarrow{a}$|=$\overrightarrow{a}$•$\overrightarrow{b}$=1,|$\overrightarrow{b}$|=2,($\overrightarrow{c}$-$\overrightarrow{a}$)•(2$\overrightarrow{c}$-$\overrightarrow{a}$-$\overrightarrow{b}$)=0,则|$\overrightarrow{c}$|的最大值为$\frac{\sqrt{19}+\sqrt{3}}{4}$.分析 由条件可以求得$<\overrightarrow{a},\overrightarrow{b}>=\frac{π}{3}$,从而可作$\overrightarrow{OA}=\overrightarrow{a},\overrightarrow{OB}=\overrightarrow{b}$,并连接AB,取AB的中点D,连接OD,则有$\overrightarrow{OD}=\frac{\overrightarrow{a}+\overrightarrow{b}}{2}$,根据条件可以得到$(\overrightarrow{c}-\overrightarrow{a})⊥(\overrightarrow{c}-\frac{\overrightarrow{a}+\overrightarrow{b}}{2})$,可作$\overrightarrow{OC}=\overrightarrow{c}$,并连接AC,DC,从而可以得到AC⊥DC,即点C在以AD为直径的圆上,从而得出当OC过圆心E时OC最大,即$|\overrightarrow{c}|$最大.而由余弦定理可以求出$AB=\sqrt{3}$,从而得出$∠OAB=\frac{π}{2}$,且$AE=CE=\frac{\sqrt{3}}{4}$,这样便可求出OE的值,进一步即可得出OC的值,即得出$|\overrightarrow{c}|$的最大值.
解答 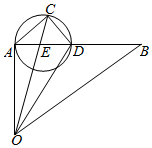 解:根据条件,$\overrightarrow{a}•\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cos<\overrightarrow{a},\overrightarrow{b}>=2cos<\overrightarrow{a},\overrightarrow{b}>=1$;
解:根据条件,$\overrightarrow{a}•\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cos<\overrightarrow{a},\overrightarrow{b}>=2cos<\overrightarrow{a},\overrightarrow{b}>=1$;
∴$cos<\overrightarrow{a},\overrightarrow{b}>=\frac{1}{2}$;
∴$<\overrightarrow{a},\overrightarrow{b}>=\frac{π}{3}$,如图,作$\overrightarrow{OA}=\overrightarrow{a},\overrightarrow{OB}=\overrightarrow{b}$,则$∠AOB=\frac{π}{3}$,连接AB,取AB的中点D,连接OD,则$\overrightarrow{OD}=\frac{\overrightarrow{a}+\overrightarrow{b}}{2}$;
由$(\overrightarrow{c}-\overrightarrow{a})•(2\overrightarrow{c}-\overrightarrow{a}-\overrightarrow{b})=0$得,$(\overrightarrow{c}-\overrightarrow{a})•(\overrightarrow{c}-\frac{\overrightarrow{a}+\overrightarrow{b}}{2})=0$;
∴$(\overrightarrow{c}-\overrightarrow{a})⊥(\overrightarrow{c}-\frac{\overrightarrow{a}+\overrightarrow{b}}{2})$;
作$\overrightarrow{OC}=\overrightarrow{c}$,连接AC,CD,则$\overrightarrow{AC}=\overrightarrow{c}-\overrightarrow{a},\overrightarrow{DC}=\overrightarrow{c}-\frac{\overrightarrow{a}+\overrightarrow{b}}{2}$;
∴AC⊥DC;
∴C点在以AD为直径的圆上;
∴当OC经过圆心E时,OC最大,即$|\overrightarrow{c}|$最大;
在△AOB中,$OA=1,OB=2,∠AOB=\frac{π}{3}$;
∴由余弦定理得,$A{B}^{2}=1+4-4×\frac{1}{2}=3$;
∴$AB=\sqrt{3}$;
∴$∠OAB=\frac{π}{2}$;
$AE=CE=\frac{\sqrt{3}}{4}$,∴$OE=\sqrt{1+\frac{3}{16}}=\frac{\sqrt{19}}{4}$;
∴$OC=OE+CE=\frac{\sqrt{19}+\sqrt{3}}{4}$;
∴$|\overrightarrow{c}|$的最大值为$\frac{\sqrt{19}+\sqrt{3}}{4}$.
故答案为:$\frac{\sqrt{19}+\sqrt{3}}{4}$.
点评 考查向量数量积的计算公式,已知三角函数求角,以及向量夹角的范围,向量的数乘运算,向量垂直的充要条件,圆的直径所对的圆周角为直角,余弦定理,直角三角形边的关系.

| A. | [-$\frac{π}{2}$+2kπ,π+2kπ],k∈Z | B. | [-$\frac{π}{2}$+3kπ,π+3kπ],k∈Z | ||
| C. | [π+2kπ,$\frac{5}{2}$π+2kπ],k∈Z | D. | [π+3kπ,$\frac{5}{2}$π+3kπ],k∈Z |
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |