题目内容
在△ABC中,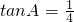 ,
,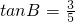 .
.
(Ⅰ)求角C的大小;
(Ⅱ)若△ABC最大边的边长为 ,求最小边的边长.
,求最小边的边长.
解:(Ⅰ)∵C=π-(A+B),∴ .--------------2'
.--------------2'
又∵0<C<π,∴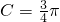 .------------------4'
.------------------4'
(Ⅱ)∵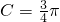 ,∴AB边最大,即
,∴AB边最大,即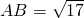 .--------------------------6'
.--------------------------6'
又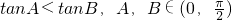 ,
,
所以∠A最小,BC边为最小边.-------------------------8'
由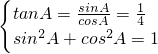 且
且 ,
,
得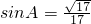 .--------------------------------10'
.--------------------------------10'
由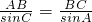 得:
得: .
.
所以,最小边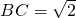 .----------------------------12'
.----------------------------12'
分析:(Ⅰ) 根据tanC=-tan(A+B),利用两角和的正切公式求出结果.
(Ⅱ)根据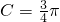 ,可得AB边最大为
,可得AB边最大为 ,又
,又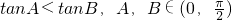 ,所以∠A最小,BC边为最小边,
,所以∠A最小,BC边为最小边,
求出sinA的值,由正弦定理求得BC的值.
点评:本题考查两角和的正切公式,正弦定理以及根据三角函数的值求角,判断∠A最小,BC边为最小边,是解题的关键.
 .--------------2'
.--------------2'又∵0<C<π,∴
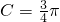 .------------------4'
.------------------4'(Ⅱ)∵
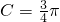 ,∴AB边最大,即
,∴AB边最大,即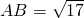 .--------------------------6'
.--------------------------6'又
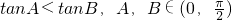 ,
,所以∠A最小,BC边为最小边.-------------------------8'
由
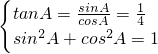 且
且 ,
,得
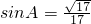 .--------------------------------10'
.--------------------------------10'由
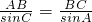 得:
得: .
.所以,最小边
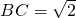 .----------------------------12'
.----------------------------12'分析:(Ⅰ) 根据tanC=-tan(A+B),利用两角和的正切公式求出结果.
(Ⅱ)根据
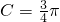 ,可得AB边最大为
,可得AB边最大为 ,又
,又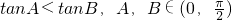 ,所以∠A最小,BC边为最小边,
,所以∠A最小,BC边为最小边,求出sinA的值,由正弦定理求得BC的值.
点评:本题考查两角和的正切公式,正弦定理以及根据三角函数的值求角,判断∠A最小,BC边为最小边,是解题的关键.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目