题目内容
已知函数f(x)=ax3+bx2经过点M(1,4),在点M处的切线恰与直线x+9y+5=0垂直.
(1)求a,b的值;
(2)若函数f(x)在区间[m-1,m+1]上单调递增,求实数m的取值范围.
解:(1)∵f(x)=ax3+bx2,
∴f′(x)=3ax2+2bx.
由已知得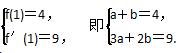
∴a=1,b=3.
(2)由(1)知f(x)=x3+3x2,
∴f′(x)=3x(x+2).
令f′(x)>0,解得x≤-2或x≥0,
∴f(x)在区间(-∞,-2]和[0,+∞)上单调递增.若f(x)在[m-1,m+1]上单调递增,
则[m-1,m+1]⊆(-∞,-2]或[m-1,m+1]⊆
[0,+∞),
∴m+1≤-2或m-1≥0.
∴m≤-3或m≥1.
∴m的取值范围是m≤-3或m≥1.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
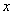 个月内,对某种商品的需求总量
个月内,对某种商品的需求总量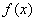 (万件)近似满足:
(万件)近似满足: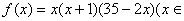 N*,且
N*,且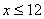 )
)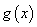 (万件)与月份
(万件)与月份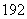 万件;
万件;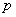 万件(不包含积压商品),要保证每月都满足供应,
万件(不包含积压商品),要保证每月都满足供应, 的图象上各点向右平移
的图象上各点向右平移 个单位,则得到新函数的解析式( )
个单位,则得到新函数的解析式( ) B.y=sin
B.y=sin C.y=sin
C.y=sin D.y=sin
D.y=sin
 ( )
( ) . ___________.
. ___________. 与椭圆C:
与椭圆C: 交于A、B两点,以OA、OB为邻边作平行四边形OAPB。
交于A、B两点,以OA、OB为邻边作平行四边形OAPB。 时,求点P的轨迹方程。
时,求点P的轨迹方程。 则不等式
则不等式 的解集为( ).
的解集为( ). B.
B.
 D.
D.
 中,
中, ,
, 表示数列
表示数列 项和,则
项和,则 ( )
( ) B.
B. C.
C. D.
D.
 的公差为
的公差为 ,数列等比数列
,数列等比数列 的公比
的公比 ,又
,又 求:①求数列
求:①求数列 ,求数列
,求数列 的前n项和
的前n项和 .
.