题目内容
直线L: 与椭圆C:
与椭圆C: 交于A、B两点,以OA、OB为邻边作平行四边形OAPB。
交于A、B两点,以OA、OB为邻边作平行四边形OAPB。
求证:椭圆C: 与直线L:
与直线L: 总有两个交点。当
总有两个交点。当 时,求点P的轨迹方程。
时,求点P的轨迹方程。
(3)是否存在直线L,使OAPB为矩形?若存在,求出此时直线L的方程;若不存在,说明理由。
解:(1)由 得
得

 椭圆C:
椭圆C: 与直线L:
与直线L: 总有两个交点。 ---------4分
总有两个交点。 ---------4分
(2)设 ,
, ,
, ,
, 与
与 交于点
交于点 ,则有
,则有
即 ,又由(1)得
,又由(1)得 ,
,

 得
得 (3)
(3)
将(3)代入(2)得

 点P的轨迹方程为
点P的轨迹方程为

由

 当
当 时,这样的直线不存在;当
时,这样的直线不存在;当 时,存在这样的直线,此时直线
时,存在这样的直线,此时直线 为
为 -
-

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 在区间上的零点的个数为 ( )
在区间上的零点的个数为 ( ) cos
cos 则cos
则cos cos
cos .
.  -
- =1交点的个数为( )
=1交点的个数为( ) 的实根所在区间为( ).
的实根所在区间为( ). B.
B.  C.
C. D.
D. 
 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,当
,当 时,有
时,有 恒成立,则不等式
恒成立,则不等式 的解集为( ).
的解集为( ). B.
B.
 D.
D.
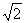 ,∠A=30°
,∠A=30° ,那么
,那么 是此数列第( )项
是此数列第( )项 C.5 D.6
C.5 D.6