题目内容
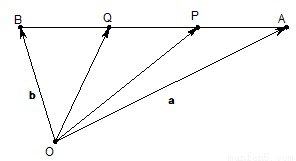
 (1)如图,设点P,Q是线段AB的三等分点,若
(1)如图,设点P,Q是线段AB的三等分点,若| OA |
| OB |
| OP |
| OQ |
(2)在(1)中,当点P,Q三等分线段AB中,有
| OP |
| OQ |
| OA |
| OB |
(3)条件同(1)(2),试用试用a,b表示向量
| OAk |
分析:(1)由题意知,
=
-
,
+
=
,从而得到
=
-
,同理求
.
(2)先写出结论,在进行证明,数形结合再利用向量加法的法则和几何意义知,
=
-
=
-
(
-
),
化简
+
+…+
的解析式,利用等差数列求和公式得到它的结果.
(3)由(2)的证明过程知,
=
-
(
-
).
| BA |
| a |
| b |
| OP |
| PA |
| OA |
| OP |
| OA |
| PA |
| OQ |
(2)先写出结论,在进行证明,数形结合再利用向量加法的法则和几何意义知,
| OAk |
| OA |
| AkA |
| a |
| k |
| n |
| a |
| b |
化简
| OA1 |
| OA2 |
| OAn-1 |
(3)由(2)的证明过程知,
| OAk |
| a |
| k |
| n |
| a |
| b |
解答:解:(1)由题意知,
=
-
,
+
=
,
∴
=
-
=
-
•(
)=
-
(
-
)=
•
+
•
.
=
-
=
-
(
-
)=
+
.
(2)能得到的结论是:
+
+…+
═
+
.
证明:
∵
=
-
=
-
(
-
)=
+
,
=
-
=
-
(
-
)=
+
,
…
=
-
=
-
(
-
)=
+
,
∴
+
+…+
=(
+
+…+
)
+(
+
+…+
)
=
+
.
(3)
=
-
=
-
(
-
)=
+
.
| BA |
| a |
| b |
| OP |
| PA |
| OA |
∴
| OP |
| OA |
| PA |
| a |
| 1 |
| 3 |
| BA |
| a |
| 1 |
| 3 |
| a |
| b |
| 2 |
| 3 |
| a |
| 1 |
| 3 |
| b |
| OQ |
| OA |
| 2 |
| 3 |
| BA |
| a |
| 2 |
| 3 |
| a |
| b |
| 1 |
| 3 |
| a |
| 2 |
| 3 |
| b |
(2)能得到的结论是:
| OA1 |
| OA2 |
| OAn-1 |
| n-1 |
| 2 |
| a |
| n-1 |
| 2 |
| b |
证明:
∵
| OA1 |
| OA |
| A1A |
| a |
| 1 |
| n |
| a |
| b |
| n-1 |
| n |
| a |
| 1 |
| n |
| b |
| OA2 |
| OA |
| A2A |
| a |
| 2 |
| n |
| a |
| b |
| n-2 |
| n |
| a |
| 2 |
| n |
| b |
…
| OAn-1 |
| OA |
| An-1A |
| a |
| n-1 |
| n |
| a |
| b |
| 1 |
| n |
| a |
| n-1 |
| n |
| b |
∴
| OA1 |
| OA2 |
| OAn-1 |
| n-1 |
| n |
| n-2 |
| n |
| 1 |
| n |
| a |
| n-1 |
| n |
| n-2 |
| n |
| 1 |
| n |
| b |
=
| n-1 |
| 2 |
| a |
| n-1 |
| 2 |
| b |
(3)
| OAk |
| OA |
| AkA |
| a |
| k |
| n |
| a |
| b |
| n-k |
| n |
| a |
| k |
| n |
| b |
点评:本题考查向量加法、减法的运算法则和几何意义,并且运用等差数列求和公式进行计算化简以及进行合情推理.

练习册系列答案
相关题目
 如图,设点P是椭圆
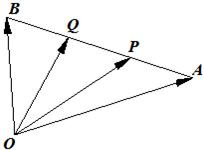
如图,设点P是椭圆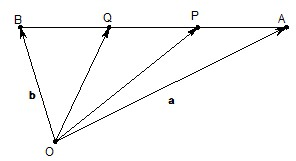 (1)如图,设点P,Q是线段AB的三等分点,若
(1)如图,设点P,Q是线段AB的三等分点,若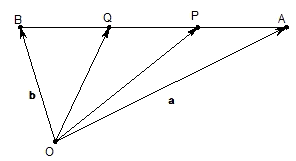 (1)如图,设点P,Q是线段AB的三等分点,若
(1)如图,设点P,Q是线段AB的三等分点,若 ,
,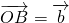 ,试用
,试用 ,
, 表示
表示 ,
,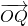 ,并判断
,并判断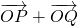 与
与 的关系;
的关系;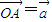 ,
,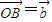 ,试用
,试用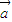 ,
,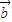 表示
表示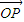 ,
,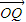 ,并判断
,并判断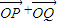 与
与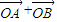 的关系;
的关系;