题目内容
在 中,角A,B,C分别所对的边为
中,角A,B,C分别所对的边为 ,且
,且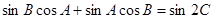 ,
, 的面积为
的面积为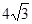 .
.
(1)求角C的大小;
(2)若 ,求边长
,求边长 .
.
(1) ;(2)
;(2)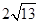
解析试题分析:(1)先用两角和的正弦公式将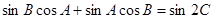 左边化为一个角的三角函数,再用三角形内角和定理及诱导公式化成sinC,右边用二倍角正弦公式展开,两边消去sinC,得到关于C的方程,从而求出C;(2)利用三角形面积公式求出b,再用余弦定理求出c.
左边化为一个角的三角函数,再用三角形内角和定理及诱导公式化成sinC,右边用二倍角正弦公式展开,两边消去sinC,得到关于C的方程,从而求出C;(2)利用三角形面积公式求出b,再用余弦定理求出c.
试题解析:(1) ,
,
化简,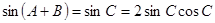
∵ ∴
∴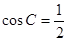 ,
,
(2)∵  的面积为
的面积为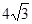 ,∴
,∴ 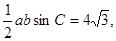 ∴
∴  .
.
又∵ ,∴
,∴  ,∴由余弦定理可得:
,∴由余弦定理可得: ,∴
,∴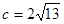
考点:三角恒等变换;三角形面积公式,余弦定理

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,
中, ,
,
 的值;
的值; 的长
的长
 中,角
中,角 所对的边为
所对的边为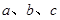 ,且满足
,且满足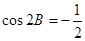 ,
, 的值;(2)若
的值;(2)若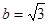 且
且 ,求
,求 的取值范围.
的取值范围.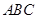 中,角
中,角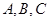 所对的边分别为
所对的边分别为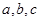 ,已知
,已知 ,
, ,
,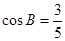 .
.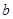 的值;
的值;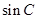 的值.
的值. 的三个内角
的三个内角 所对的边分别为
所对的边分别为 ,向量
,向量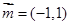 ,
, ,且
,且 .
. 的大小;
的大小;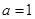 ;②
;② ;③
;③ ,试从中再选择两个条件以确定
,试从中再选择两个条件以确定 分别为内角A,B,C的对边,且
分别为内角A,B,C的对边,且
 ,试判断△ABC的形状.
,试判断△ABC的形状. 中,已知
中,已知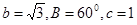 ,解三角形
,解三角形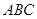 .
. 中,
中, ,
,
 的值;
的值; 的长
的长