题目内容
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|>0),在同一周期内,当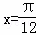 时,f(x)取得最大值3;当
时,f(x)取得最大值3;当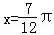 时,f(x)取得最小值﹣3.
时,f(x)取得最小值﹣3.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)求函数f(x)的单调递减区间;
(Ⅲ)若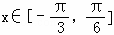 时,函数h(x)=2f(x)+1﹣m有两个零点,求实数m的取值范围.
时,函数h(x)=2f(x)+1﹣m有两个零点,求实数m的取值范围.
解:(Ⅰ)由题意可得A=3,周期T=2(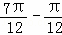 )=
)=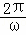 ,∴ω=2.
,∴ω=2.
由2×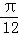 +φ=2kπ+
+φ=2kπ+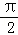 ,k∈z,以及﹣π<φ<π,可得 φ=
,k∈z,以及﹣π<φ<π,可得 φ=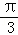 ,故函数f(x)=3sin(2x+
,故函数f(x)=3sin(2x+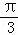 ).
).
(Ⅱ)由 2kπ+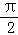 ≤2x+
≤2x+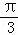 ≤2kπ+
≤2kπ+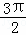 ,k∈z,求得kπ+
,k∈z,求得kπ+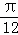 ≤x≤kπ+
≤x≤kπ+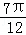 ,
,
故函数的减区间为[kπ+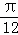 ,kπ+
,kπ+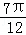 ],k∈z.
],k∈z.
(Ⅲ)∵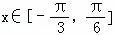 时,函数h(x)=2f(x)+1﹣m有两个零点,故 sin(2x+
时,函数h(x)=2f(x)+1﹣m有两个零点,故 sin(2x+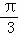 )=
)=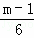 有2个实数根.
有2个实数根.
即函数y=sin(2x+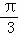 )的图象和直线y=
)的图象和直线y=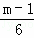 有2个交点.
有2个交点.
再由 2x+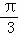 ∈[﹣
∈[﹣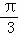 ,
,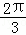 ],结合函数y=sin(2x+
],结合函数y=sin(2x+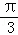 )的图象可得
)的图象可得 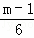 ∈[
∈[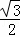 ,1),解得 m∈[3
,1),解得 m∈[3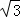 +1,7),
+1,7),
即 实数m的取值范围是[3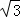 +1,7).
+1,7).

练习册系列答案
相关题目
 中,三内角
中,三内角 成等差数列,则
成等差数列,则 的最大值为 ( )A.
的最大值为 ( )A. B.
B. C.
C. D.
D.
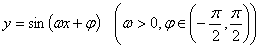 的最小正周期为
的最小正周期为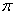 ,且其图象关于直线
,且其图象关于直线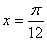 对称, 则在下面四个结论:
对称, 则在下面四个结论: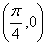 对称; ②图象关于点
对称; ②图象关于点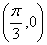 对称;
对称;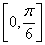 上是增函数; ④在
上是增函数; ④在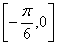 上是增函数中,
上是增函数中,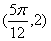 在函数
在函数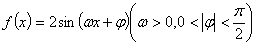 的图象上,直线
的图象上,直线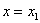 、
、 是
是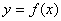 图象的任意两条对称轴,且
图象的任意两条对称轴,且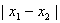 的最小值为
的最小值为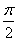 .
.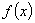 的单递增区间和其图象的对称中心坐标;
的单递增区间和其图象的对称中心坐标;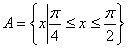 ,
, ,若
,若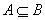 ,求实数
,求实数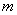 的取值范围.
的取值范围. 上有意义,且在
上有意义,且在 上单调递减,
上单调递减, 。又
。又 。若集合
。若集合

 、
、 、
、 为
为 的三内角,且其对边分别为
的三内角,且其对边分别为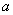 、
、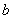 、
、 ,若
,若 .
. ,求
,求 ,给出M到N的映射
,给出M到N的映射 ,则点
,则点 的象
的象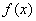 的最小正周期是( )
的最小正周期是( )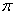 B.
B. C.
C. D.
D.
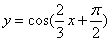 是奇函数; ②存在实数
是奇函数; ②存在实数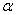 ,使得
,使得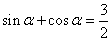 ; ③若
; ③若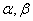 是第一象限角且
是第一象限角且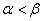 ,则
,则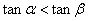 ; ④
; ④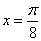 是函数
是函数 的一条对称轴方程;⑤函数
的一条对称轴方程;⑤函数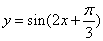 的图像关于点
的图像关于点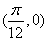 成中心对称.把你认为正确的命题的序号都填在横线上______________.
成中心对称.把你认为正确的命题的序号都填在横线上______________. 有且仅有两个不同的实数解
有且仅有两个不同的实数解 ,则以下有关两根关系的结论正确的是( )
,则以下有关两根关系的结论正确的是( ) B.
B.
 D.
D.