题目内容
14.已知向量$\overrightarrow{a}$=(sinθ,-2)与$\overrightarrow{b}$=(1,cosθ)互相垂直,其中θ∈$(0,\frac{π}{2})$,则sinθ+cosθ等于( )| A. | $\frac{{-\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{{3\sqrt{5}}}{5}$ |
分析 由$\overrightarrow{a}⊥\overrightarrow{b}$,可得$\overrightarrow{a}•\overrightarrow{b}$=sinθ-2cosθ=0,tanθ=2.可得sinθcosθ=$\frac{sinθcosθ}{si{n}^{2}θ+co{s}^{2}θ}$=$\frac{tanθ}{ta{n}^{2}θ+1}$.由于θ∈$(0,\frac{π}{2})$,可得sinθ+cosθ=$\sqrt{(sinθ+cosθ)^{2}}$=$\sqrt{1+2sinθcosθ}$.
解答 解:∵$\overrightarrow{a}⊥\overrightarrow{b}$,
∴$\overrightarrow{a}•\overrightarrow{b}$=sinθ-2cosθ=0,
∴tanθ=2.
∴sinθcosθ=$\frac{sinθcosθ}{si{n}^{2}θ+co{s}^{2}θ}$=$\frac{tanθ}{ta{n}^{2}θ+1}$=$\frac{2}{{2}^{2}+1}$=$\frac{2}{5}$.
∵θ∈$(0,\frac{π}{2})$,
∴sinθ+cosθ=$\sqrt{(sinθ+cosθ)^{2}}$=$\sqrt{1+2sinθcosθ}$=$\sqrt{1+2×\frac{2}{5}}$=$\frac{3\sqrt{5}}{5}$.
故选:D.
点评 本题考查了向量数量积运算性质、同角三角函数基本关系式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
9.已知数列{an}的通项an=$\frac{nx}{(x+1)(2x+1)…(nx+1)}$,n∈N*,若a1+a2+a3<1,则实数x可能等于( )
| A. | -$\frac{3}{2}$ | B. | -$\frac{5}{12}$ | C. | -$\frac{4}{7}$ | D. | -$\frac{11}{24}$ |
19.在复平面内,复数$\frac{1}{1+i}-\frac{1}{3}{i^7}$对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
6.若lg2=a,lg3=b,则log23等于( )
| A. | $\frac{b}{a}$ | B. | $\frac{a}{b}$ | C. | ab | D. | ba |
4.已知函数f(x)=$\sqrt{3}$sinωx+cosωx(ω>0)在区间[-ω,ω]上单调递增,且函数f(x)的图象关于直线x=ω对称,则ω的值为( )
| A. | $\frac{\sqrt{π}}{3}$ | B. | $\frac{\sqrt{π}}{2}$ | C. | $\frac{\sqrt{3π}}{3}$ | D. | $\frac{\sqrt{3π}}{2}$ |
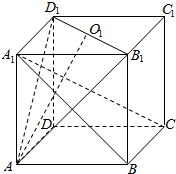 已知点O1是正方体ABCD-A1B1C1D1的上底面的中心,求证:对角线A1C与平面AD1B1的交点P一定在AO1上.
已知点O1是正方体ABCD-A1B1C1D1的上底面的中心,求证:对角线A1C与平面AD1B1的交点P一定在AO1上.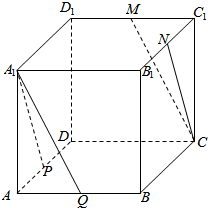 在正方体ABCD-A1B1C1D1中,P,Q,M,N分别为AD,AB,C1D1,B1C1的中点,求证:
在正方体ABCD-A1B1C1D1中,P,Q,M,N分别为AD,AB,C1D1,B1C1的中点,求证: